Buscador global
Mostrando del 2801 al 2810 de 3589 resultados filtrando por: Propuesta didáctica
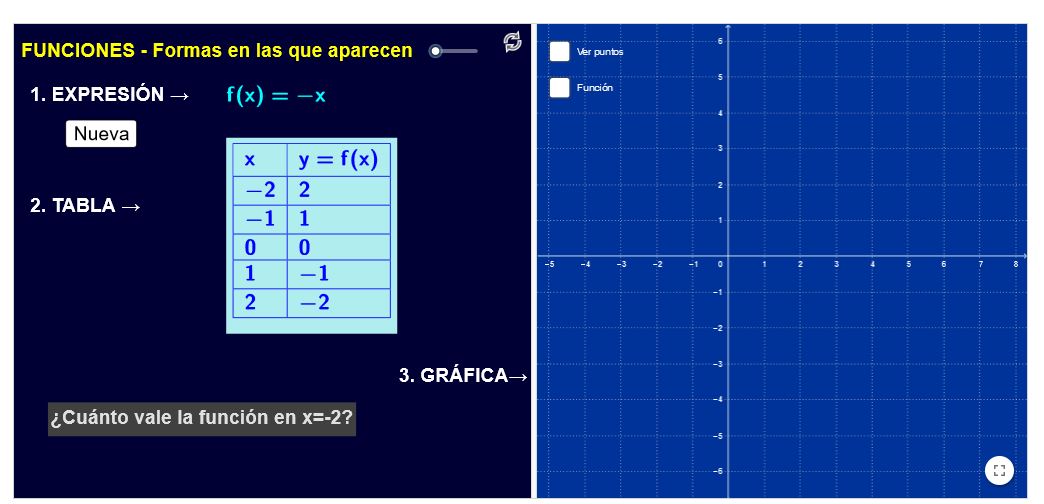
Funciones-Formas en las que aparecen
Relación entre expresión algebraica, tabla y gráfica de funciones lineales y cuadráticas
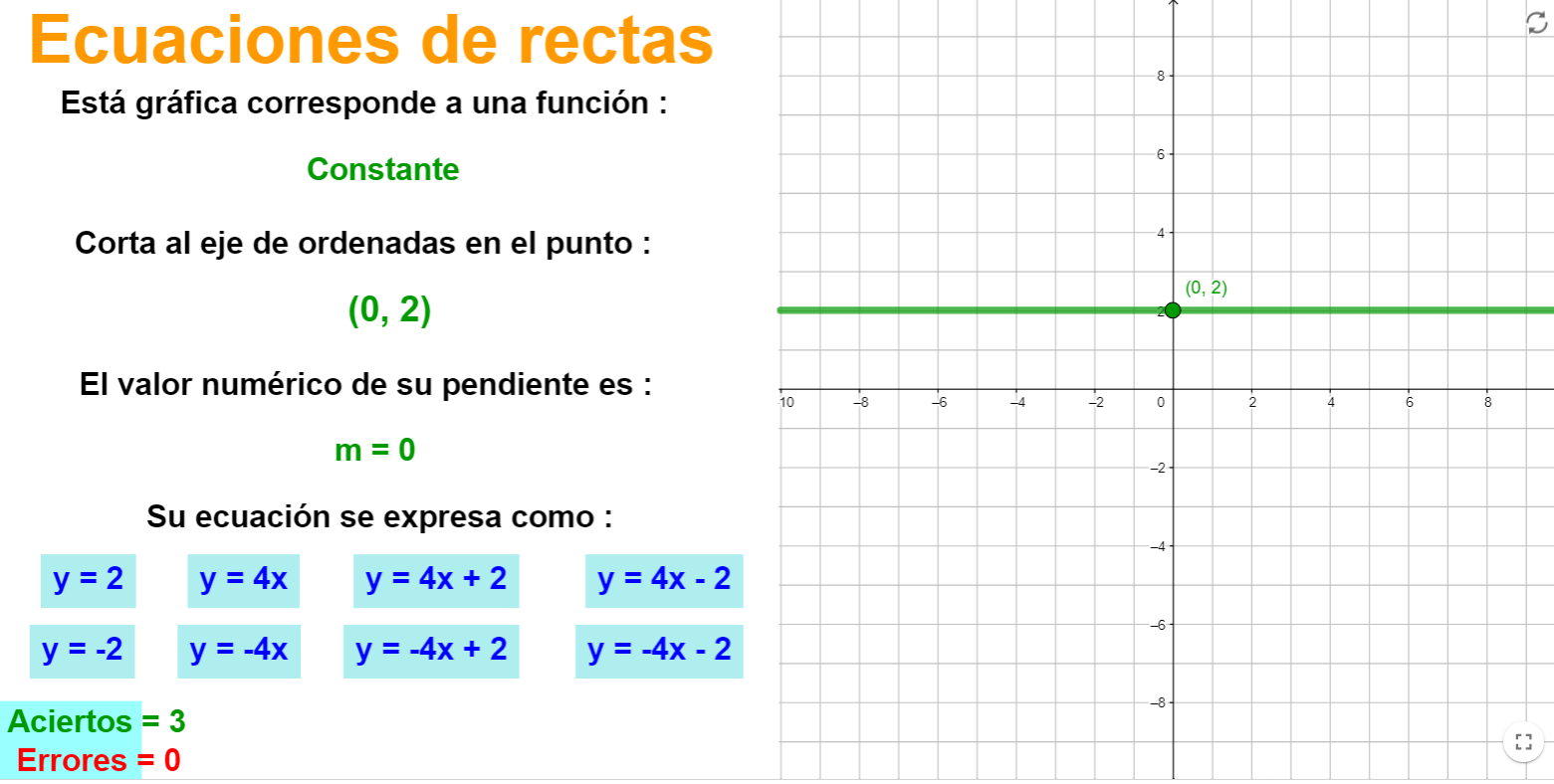
Ecuaciones de rectas
Dada la gráfica de una recta (oblicua o horizontal) se trata de identificar su pendiente, el punto de corte con el eje Y, su ecuación y el tipo de función asociada a dicha gráfica (de proporcionalidad, constante o afín).
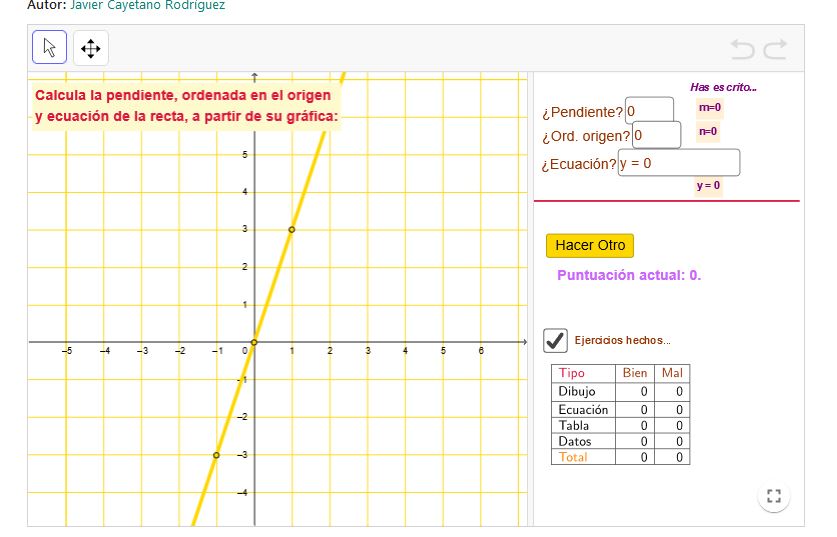
La recta. Pendiente y ordenada en el origen
Con esta actividad se practican los conceptos de pendiente y ordenada en el origen de rectas, las cuales pueden venir dadas mediante su representación gráfica, su ecuación o mediante una tabla de valores. También se practica la representación gráfica de la recta dada su ecuación y la obtención de puntos de esta.
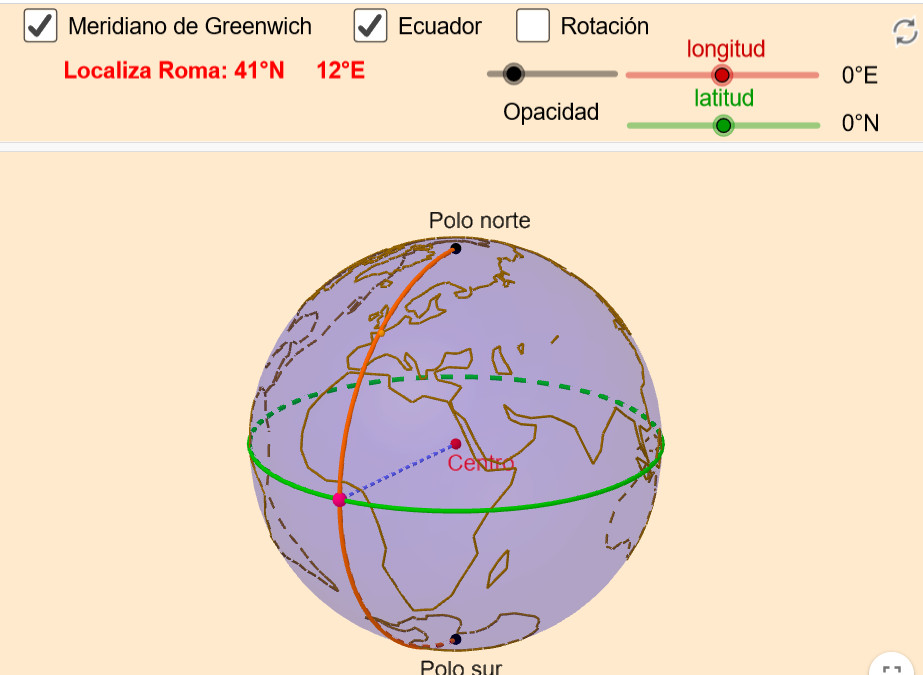
Coordenadas geográficas: localizando ciudades
Applet de GeoGebra que presenta una esfera sobre la que se han dibujado los continentes podemos desplazar un punto mediante dos deslizadores que controlan la longitud y la latitud.

Intersección esfera-plano
Applet de Geogebra que presenta distintas formas de cortar una esfera, un cilindro y un cono con un plano que podemos colocar en distintas posiciones y orientaciones.

Visualización espacial
Applet de Geogebra que presenta distintas formas de cortar una esfera, un cilindro y un cono con un plano que podemos colocar en distintas posiciones y orientaciones.
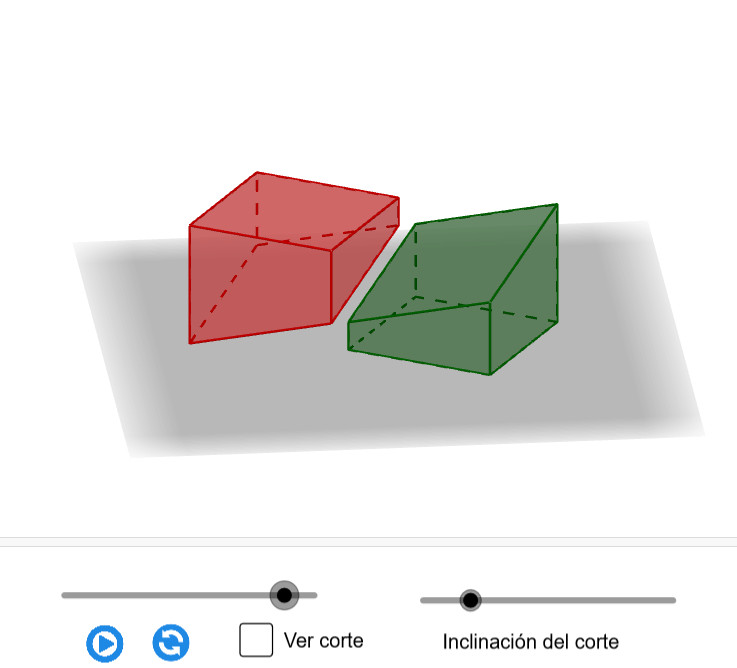
Mitad del cubo. Rombos
El applet muestra la sección que se produce en un cubo cuando lo cortamos con un plano que pasa por una de sus diagonales espaciales y los puntos medios de dos aristas opuestas dando lugar a un rombo. Se puede modificar la inclinación del corte para obtener otros polígonos.
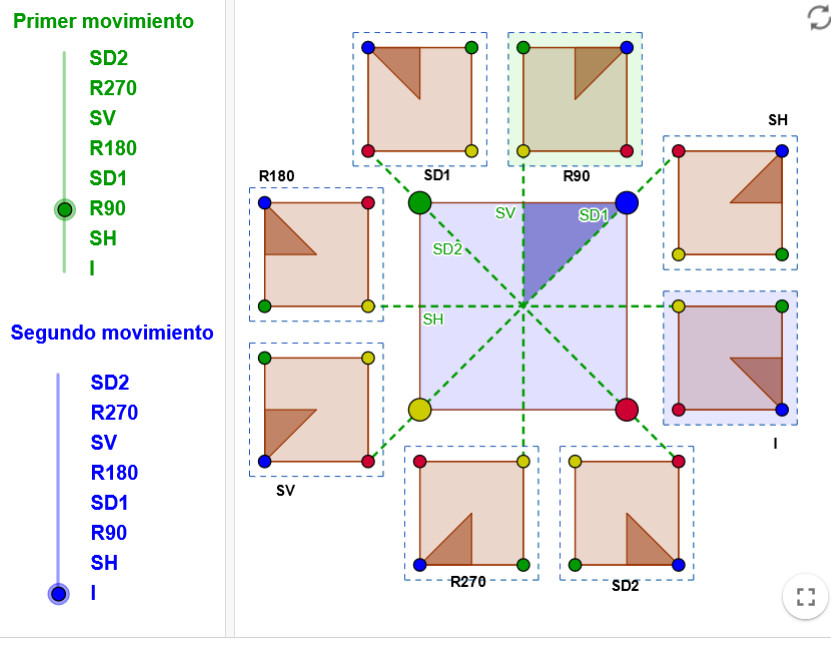
Grupo de simetría del cuadrado
Applet de Geogebra que presenta las ocho simetrías de un cuadrado y propone estudiar la composición de cada dos simetrías para llegar a la estructura de grupo.
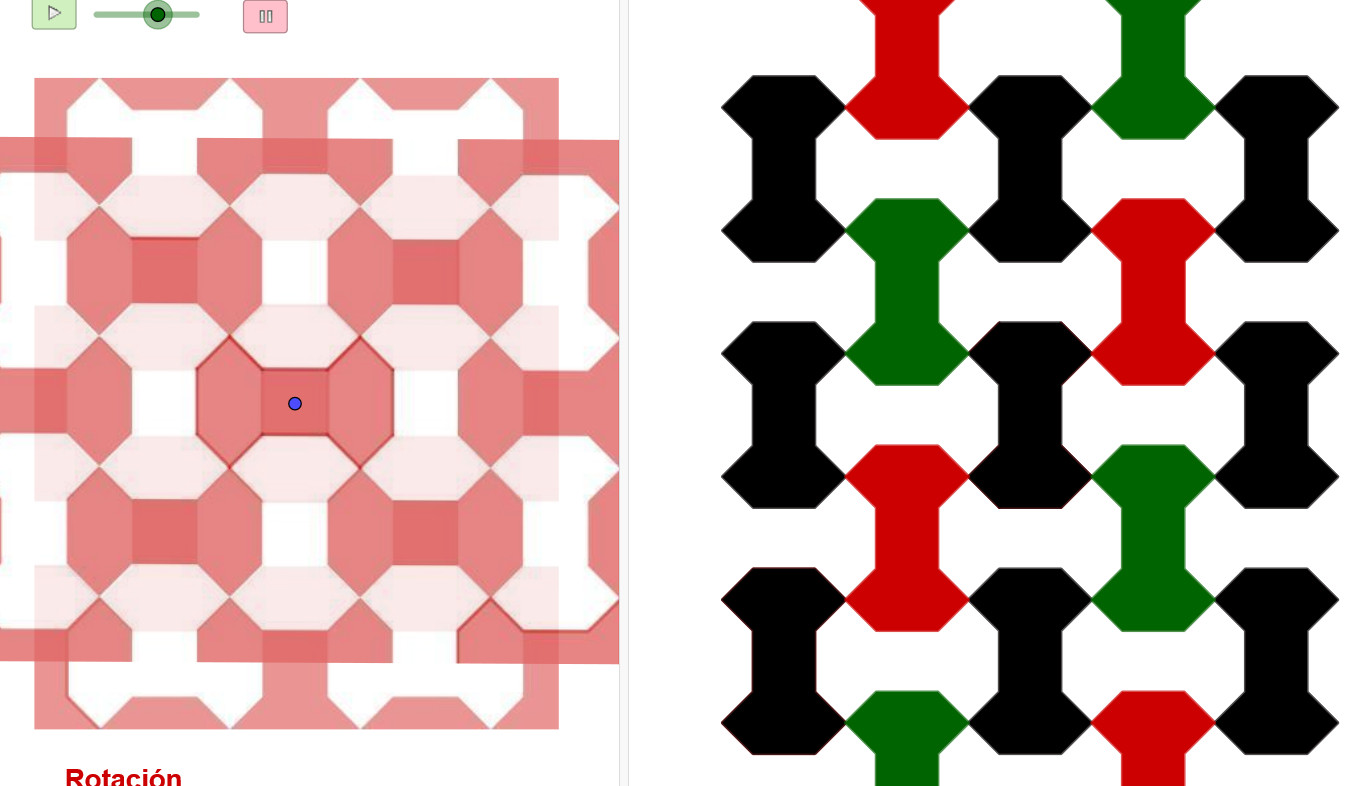
El hueso y los movimientos en un mosaico
Applet de Geogebra que presenta una secuencia animada para construir la baldosa del hueso, después con la baldosa se diseña el mosaico y se termina con el estudio de las simetrías de la composición.
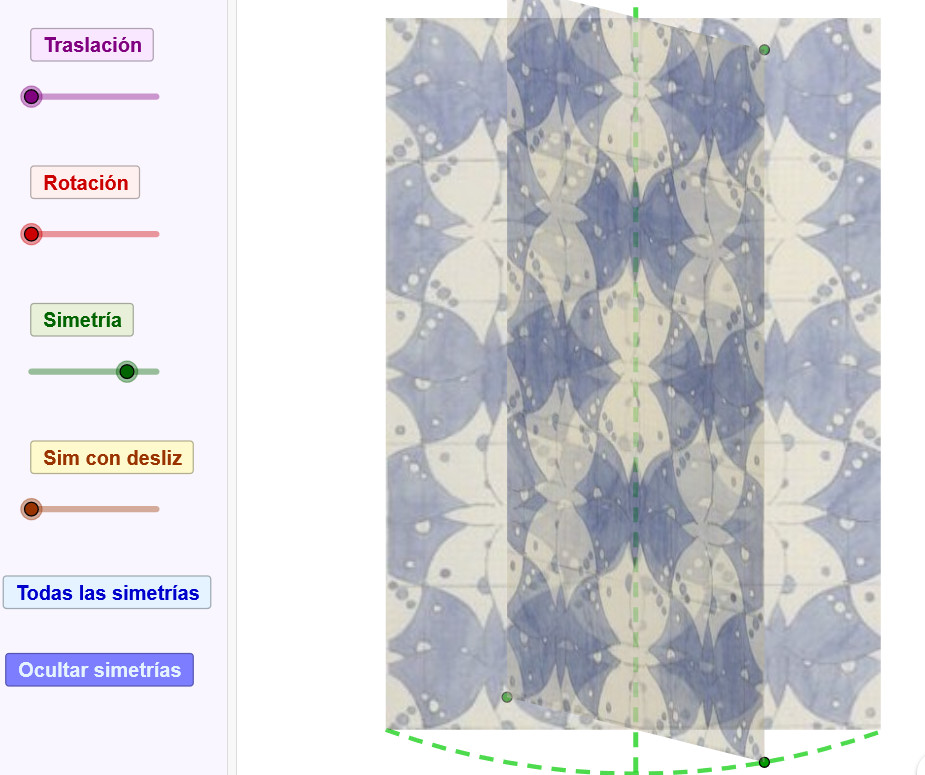
Los cuatro movimientos en un mosaico. Escher
Applet de Geogebra que presenta un mosaico de M. C. Escher y aplica en él los cuatro movimientos en el plano utilizando referentes físicos como deslizar para la traslación o dar la vuelta para la simetría.