Buscador global
Mostrando del 11 al 20 de 26 resultados filtrando por: Parábola
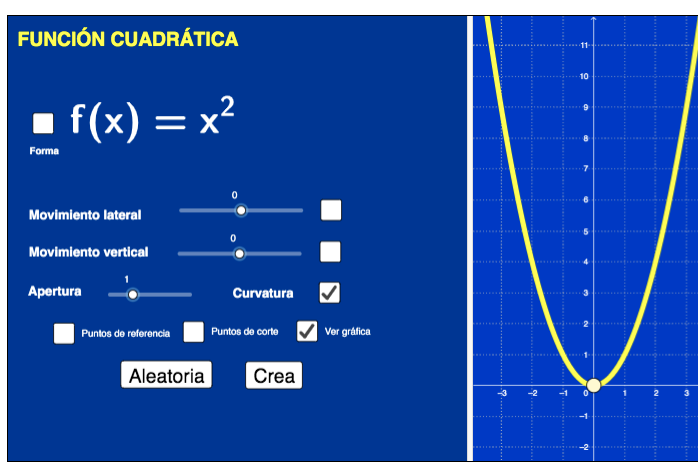
Función cuadrática: movimientos
Se plantea estudiar la gráfica de funciones cuadráticas a partir de transformaciones de la función cuadrática simple y=x^2. Con ello se pretende que el alumno aprecie el efecto de los coeficientes de la función en la gráfica.
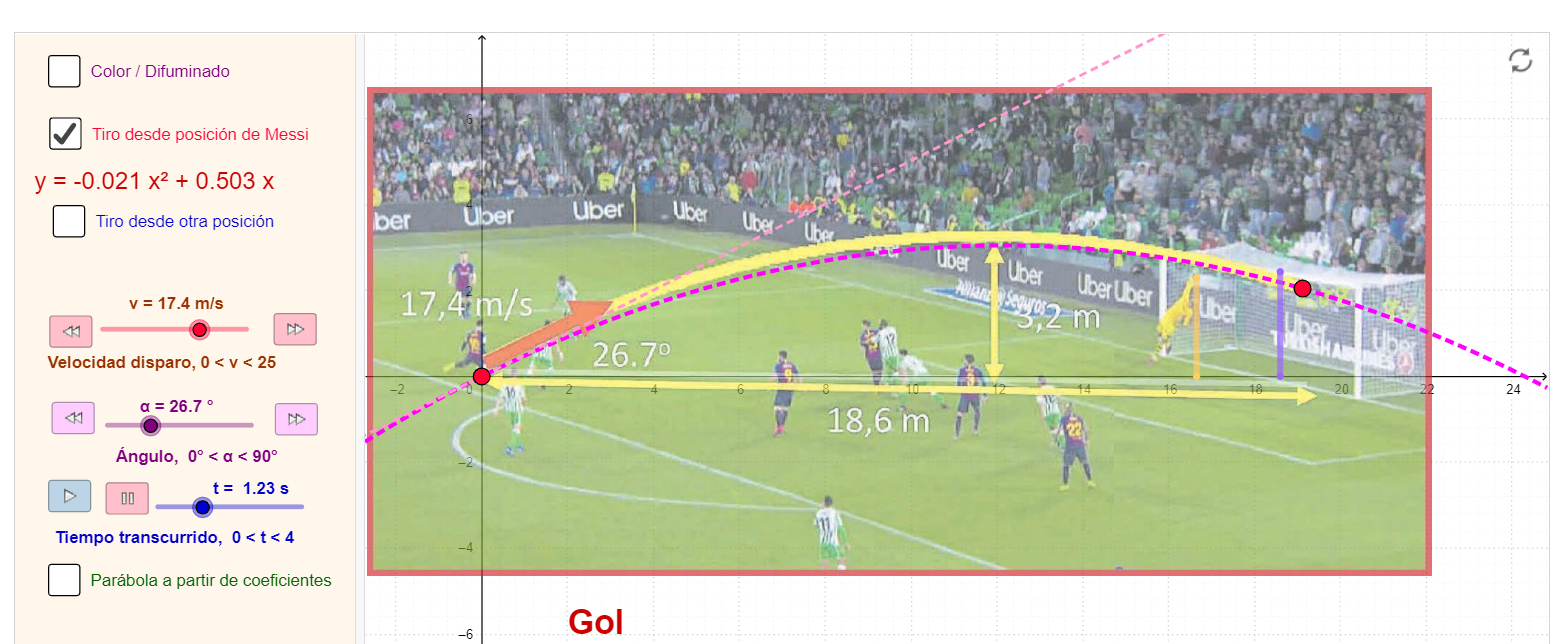
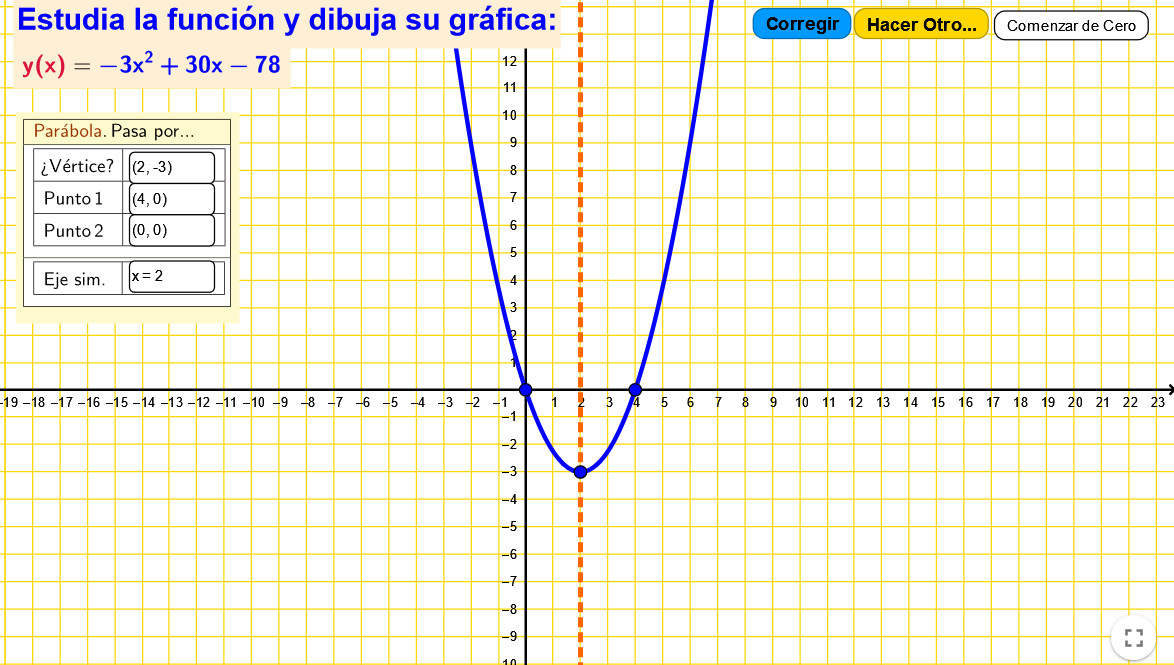
Parábolas y fútbol
Analizando un disparo a portería en un partido de fútbol, se estudia la trayectoria parabólica. Además se propone profundizar más hallando las ecuaciones de movimiento.
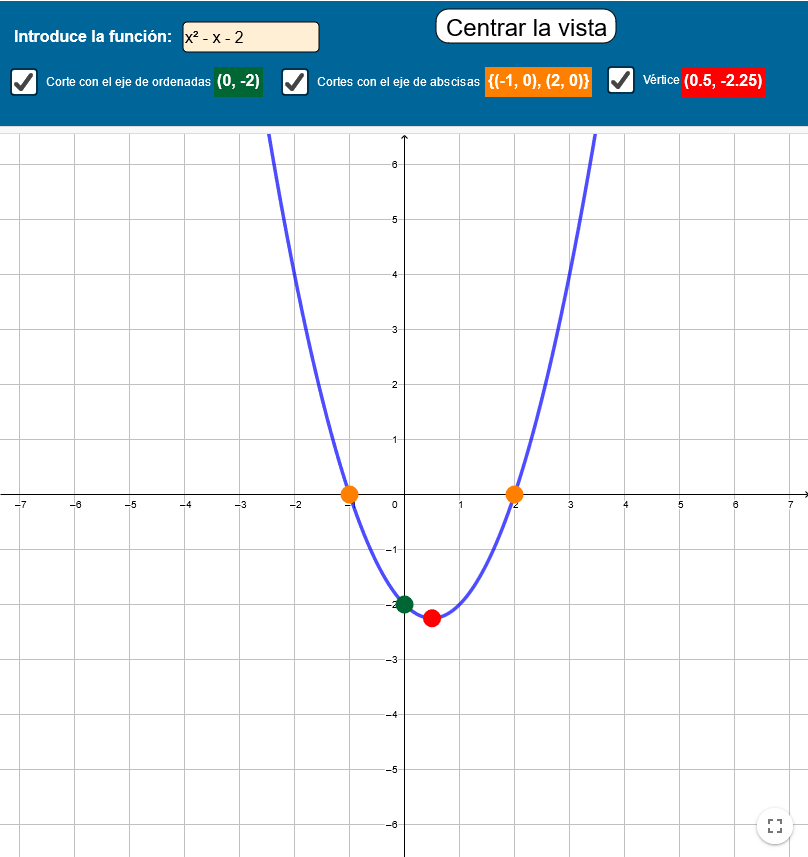
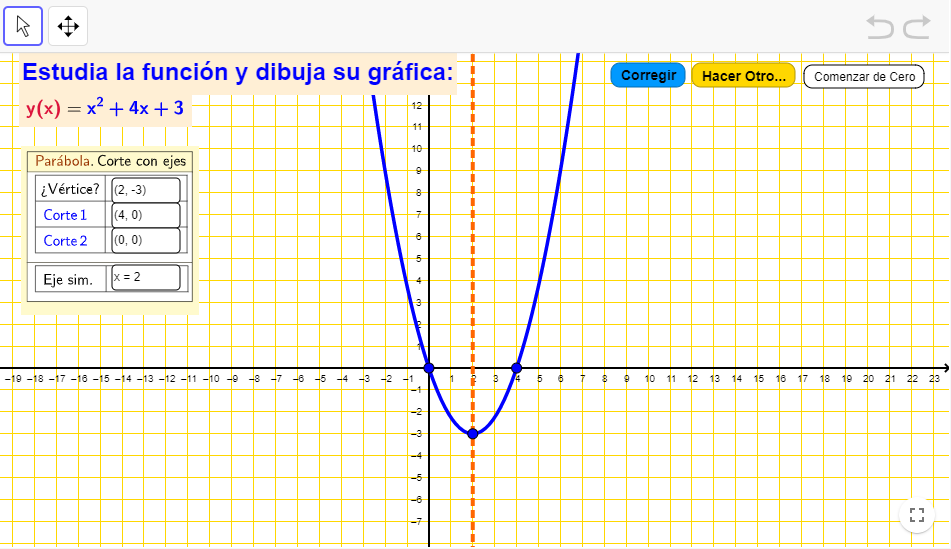
Representación de parábolas
Actividad básica. Introduciendo la expresión de una función cuadrática, la representa y muestra los puntos.
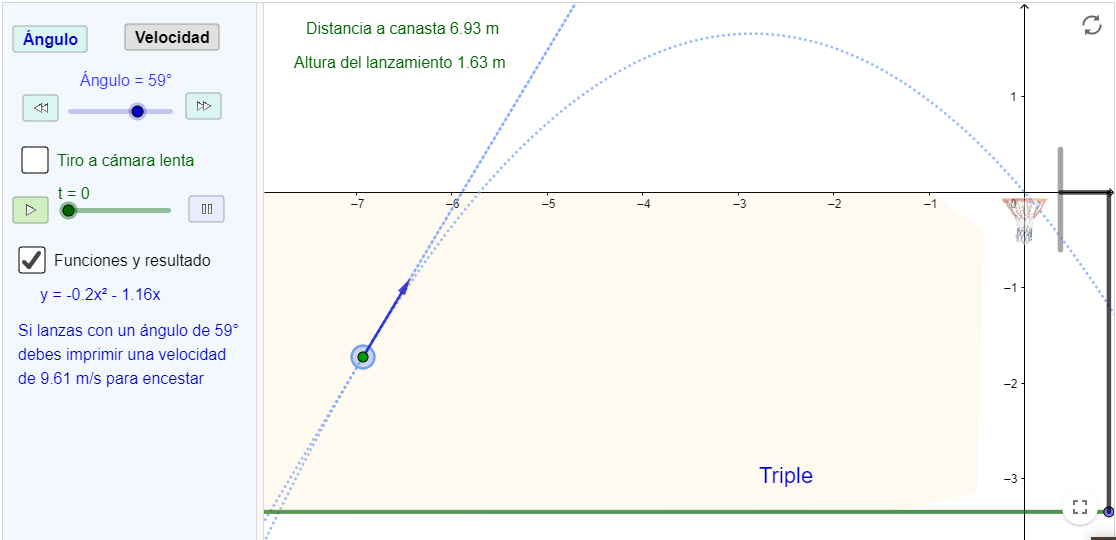
Lanzamiento a canasta. Parábolas
La aplicación simula un tiro a canasta en el que podemos modificar las condiciones del lanzamiento. Se pueden observar la expresión algebraica, los ángulos de inclinación y la altura. Contiene un estudio amplio de las velocidades.
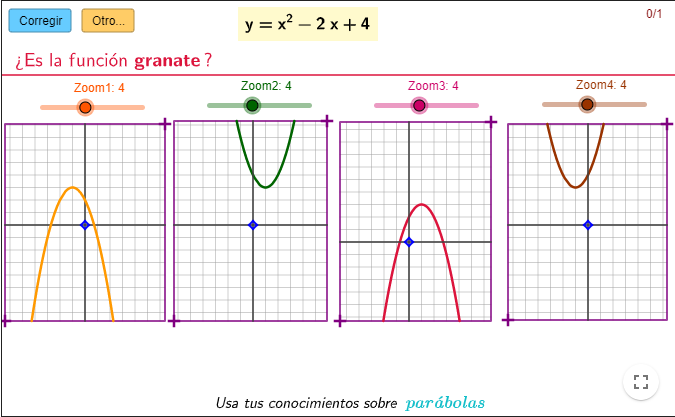
Parábolas. Elige la función correcta
En este recurso se nos da la expresión algebraica de una función cuadrática y el alumno debe elegir entre cuatro posibles gráficas cuál se corresponde la expresión dada.
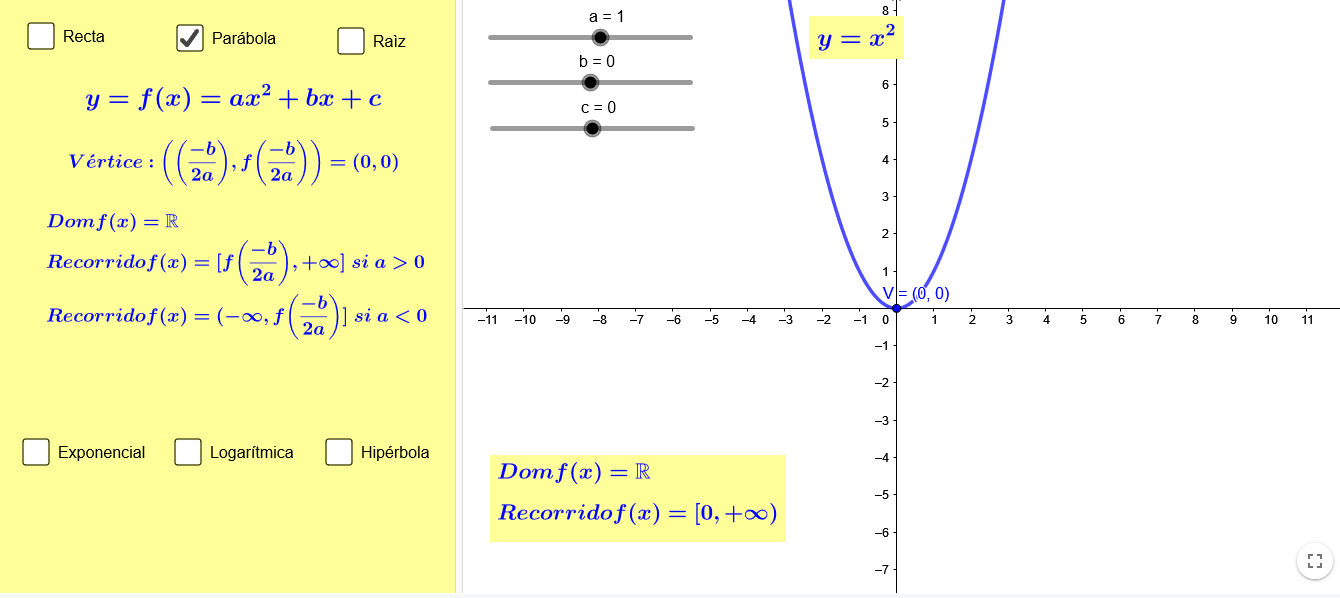
Funciones elementales
Se proponen 6 familias de funciones a elegir (recta, parábola, raíz, exponencial, logarítmica, hipérbola), y se modifican los parámetros que aparecen observando su acción sobre la gráfica. También aparece el dominio y recorrido de la función y algunas particularidades como pendiente (recta) o vértice (parábola).
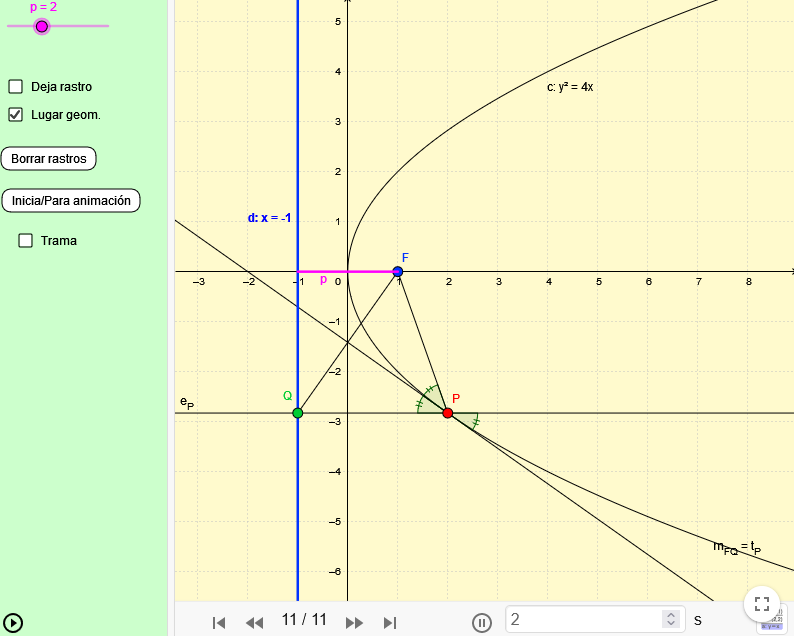
Generación de la parábola como lugar geométrico
Permite entender paso a paso el proceso de construcción de la parábola como lugar geométrico de los puntos del plano que equidistan de un punto y de una recta fijados previamente. Define el concepto de foco, vértice y parámetro, pero no entra en el desarrollo de la ecuación; el objetivo es entender perfectamente la construcción geométrica de la parábola.
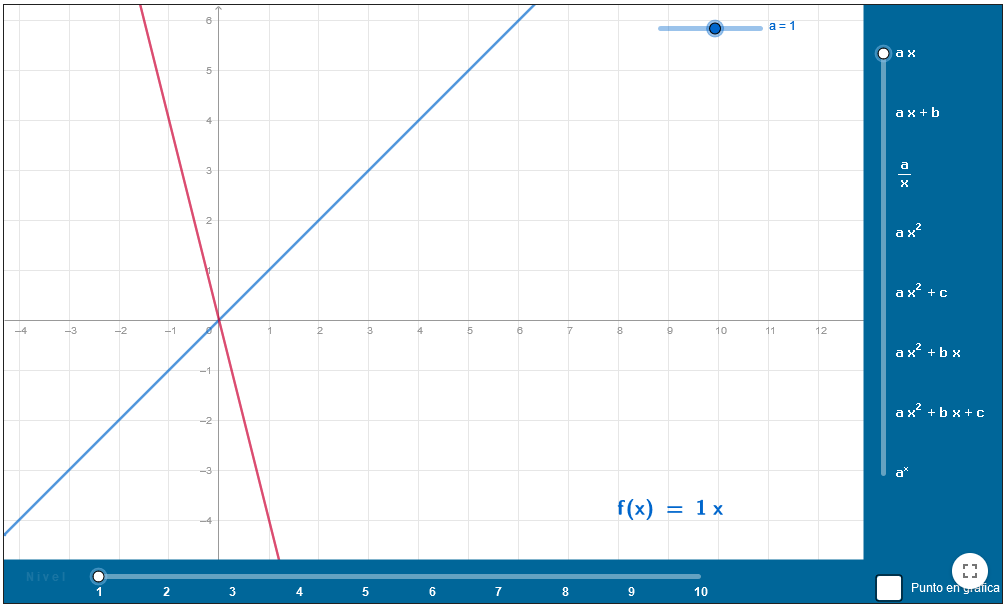
El juego de las funciones
Juego que permite asociar gráficas de funciones elementales con su ecuación. Hay que elegir la familia de funciones adecuada y mover los deslizadores hasta hallar los parámetros.