Buscador global
Mostrando del 1 al 10 de 27 resultados filtrando por: Matriz
Conexiones de telefonía fija
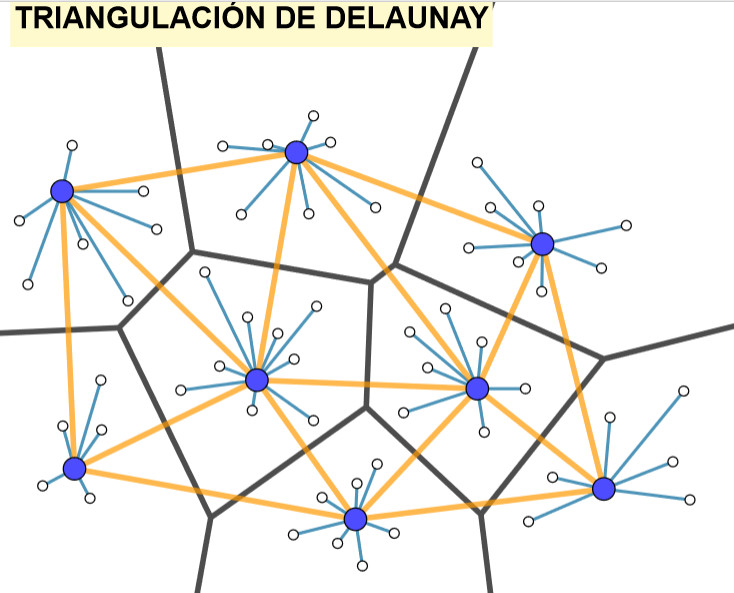
A partir de una colección de puntos crea el diagrama de Voronoi, el diagrama de Delaunay, las posibles conexiones y el recorrido mínimo. La actividad forma parte de un libro más amplio dedicado a Redes y Grafos.

Matrices de Leslie
La actividad presenta una aplicación práctica de las matrices: El modelo poblacional de Leslie. La matriz va a describir la evolución de la población dependiendo de la tasa de fertilidad de las hembras y la probabilidad de supervivencia. La magnitud del valor propio positivo de la matriz determinará que la población se extinga, aumente indefinidamente o se estabilice.

Cadenas de Markov
En la actividad se presentan las cadenas de Markov como ejemplo de aplicación de las matrices. El applet pide los elementos de la matriz estocástica P y calcula sus potencias para ver el estado final al cabo de n periodos. También aparece el comportamiento asintótico de la cadena.
Chifré de Hill
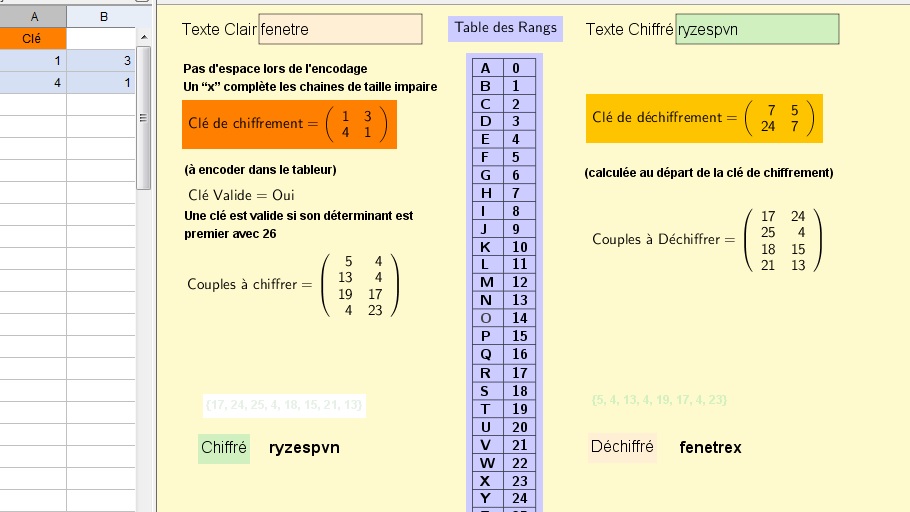
En la actividad se presenta el cifrado de Hill como ejemplo de aplicación de las matrices. El applet pide los elementos de la matriz 'Clé de chifrement', que hay que introducir en la vista hoja de cálculo. A partir de ahí introducimos un mensaje corto y se devuelve codificado. Además, se intuye la utilización de la inversa para la decodificación.

Ecuaciones matriciales
El applet resuelve un buen abanico de ecuaciones con matrices. Para cada terna de matrices, propone 6 ecuaciones distintas que se resuelven paso a paso mediante el botón "Solución". Podemos variar las matrices de partida mediante el botón "Nuevo".
Matrices de conexiones
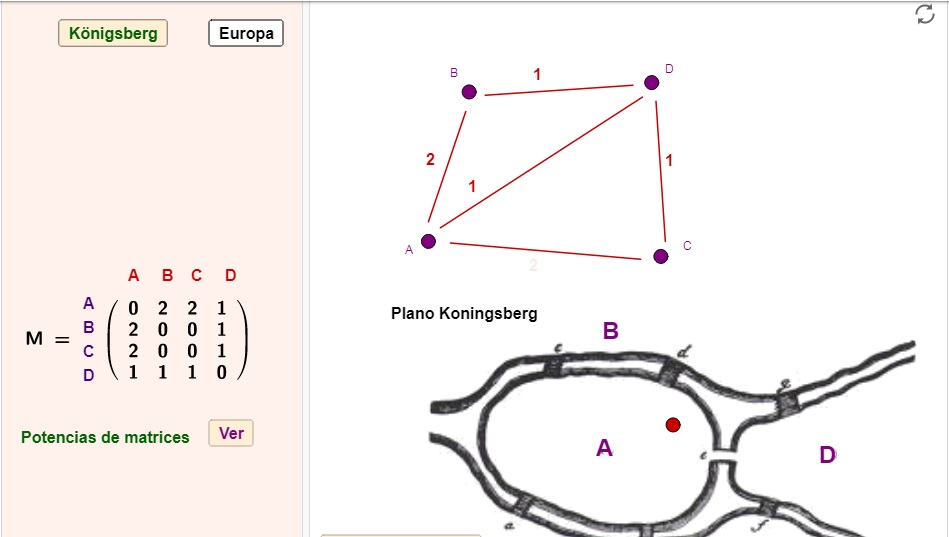
El applet presenta el conocido problema de los puentes de Königsberg, resuelto por Leonhard Euler en 1736 y cuya resolución dio origen a la teoría de grafos. Se plantea una matriz (M) que indica el número de puentes que es posible cruzar para pasar de un sector a otro. Se pide la interpretación de las potencias de M y resolver el problema inicial: ¿Hay un recorrido para cruzar a pie toda la ciudad, pasando por todos los puentes pero sólo una vez por cada uno?

Producto de Matrices
El applet detalla, a través de ejemplos aleatorios cómo se hace el producto de dos matrices. El alumnado va eligiendo la fila de la primera matriz (i) y la columna de la segunda (j), para obtener el elemento (i,j) de la matriz producto. El grafo ayuda a que el algoritmo sea aprendido.

Inverse Matrix
El applet repasa el cálculo de la matriz inversa, especificando todo los pasos: cálculo del determinante, cálculo de la matriz adjunta, de la adjunta traspuesta, y al final, de la inversa. Introducimos la matriz por sus elementos y salen los cálculos de forma ordenada.

Vectores y matrices
El applet muestra la equivalencia entre las combinaciones lineales de vectores de R^3 y el rango de la matriz cuadrada de orden 3 correspondiente. Los 3 deslizadores son los coeficientes de la combinación lineal y vemos que x_1 u+x_2 v+x_3 w siempre coincide con la operación matricial A x.
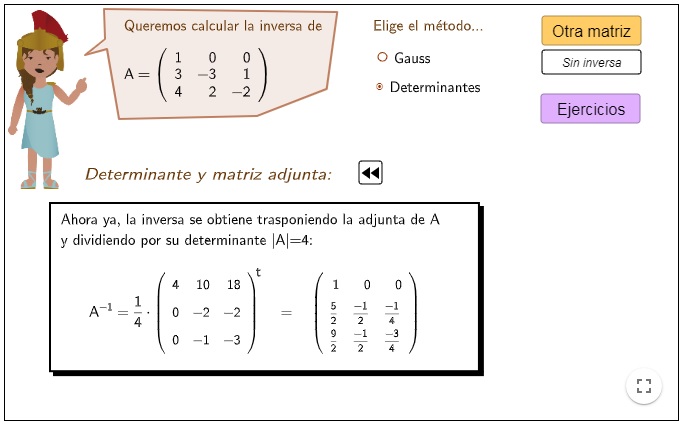
Inversa de una matriz 3×3
La actividad explica paso a paso el cálculo de la inversa de una matriz, ya sea por el Método de Gauss o por determinantes. Plantea ejemplos de forma aleatoria y acaba proponiendo varios ejercicios que se autocorrigen, otorgando una puntuación dependiendo de los aciertos.