Buscador global
Mostrando del 1111 al 1120 de 1412 resultados filtrando por: MatesGG
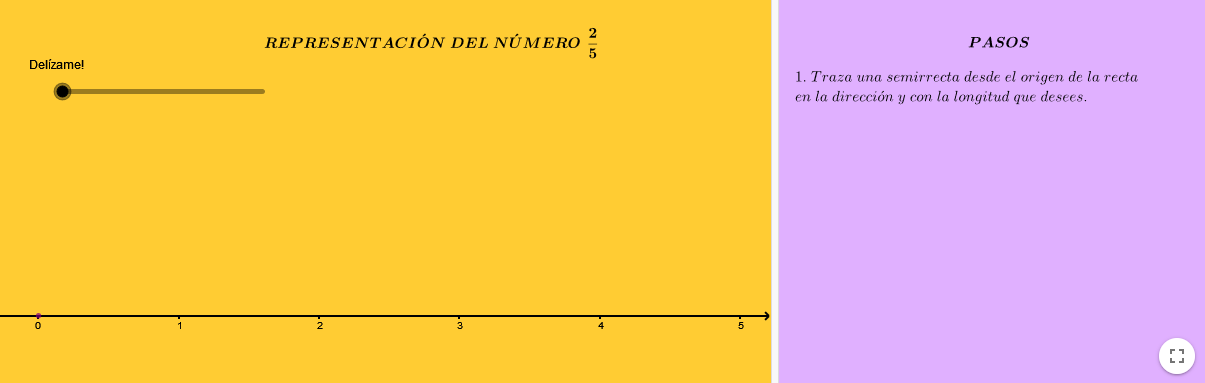
Representación de números racionales
Visualización paso a paso de cómo representar números racionales en la recta real.
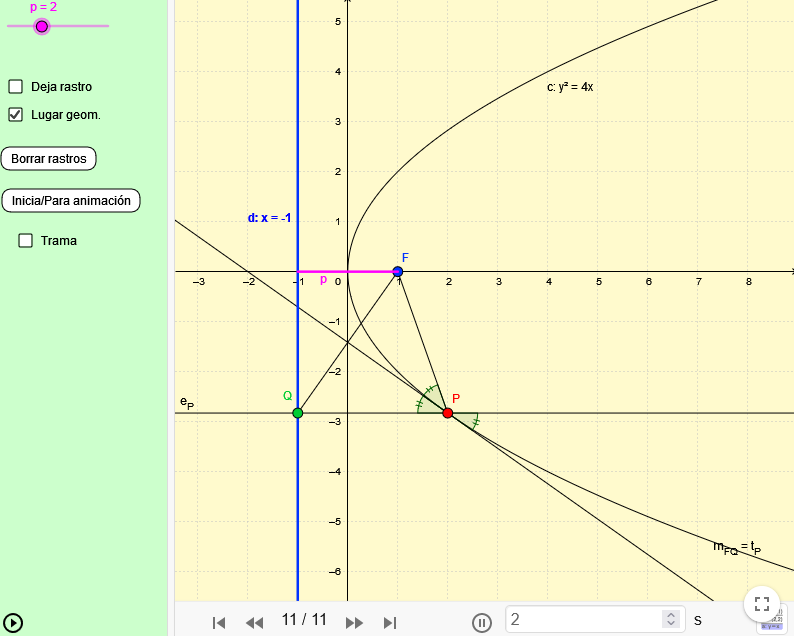
Generación de la parábola como lugar geométrico
Permite entender paso a paso el proceso de construcción de la parábola como lugar geométrico de los puntos del plano que equidistan de un punto y de una recta fijados previamente. Define el concepto de foco, vértice y parámetro, pero no entra en el desarrollo de la ecuación; el objetivo es entender perfectamente la construcción geométrica de la parábola.
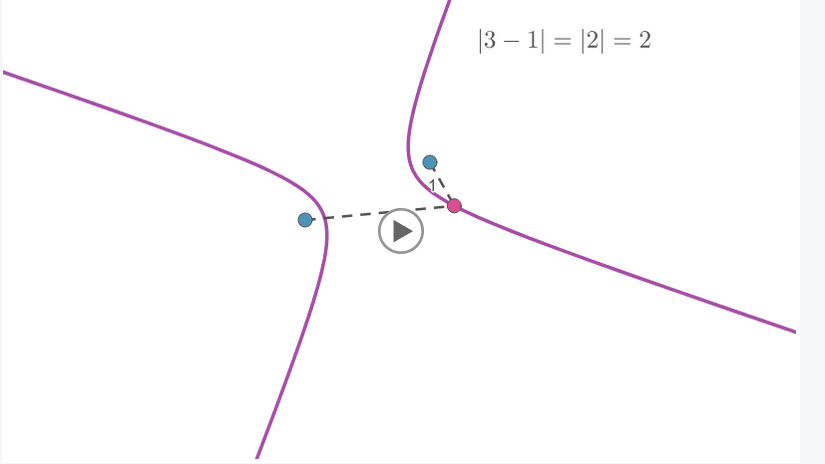
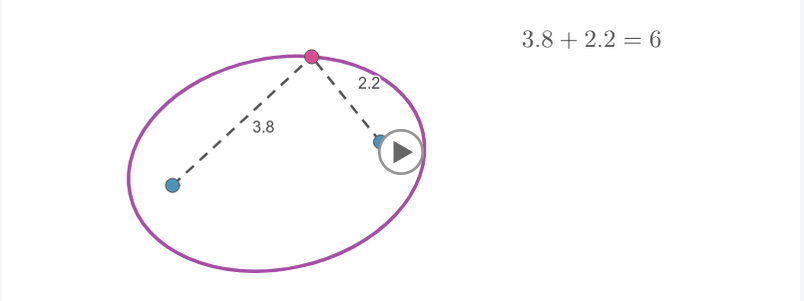
La hipérbola
Presenta la definición de hipérbola como el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos (focos) es constante. Propone encontrar la ecuación de la hipérbola a partir de esta definición.
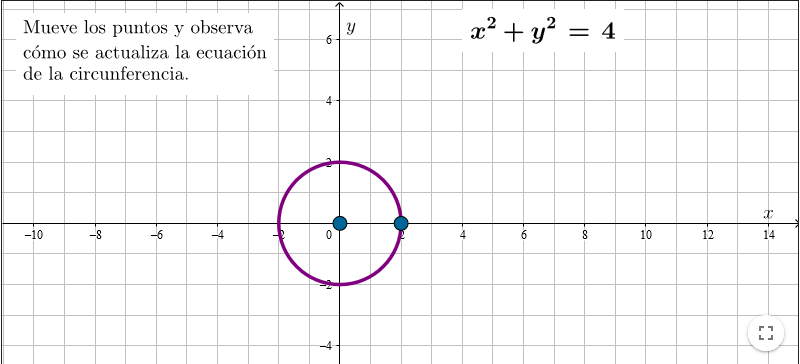
La circunferencia
Presenta la definición de circunferencia como lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Propone encontrar la ecuación de la circunferencia a partir de esta definición. Permite observar cómo varía la ecuación al cambiar el centro o la distancia de los puntos al centro.
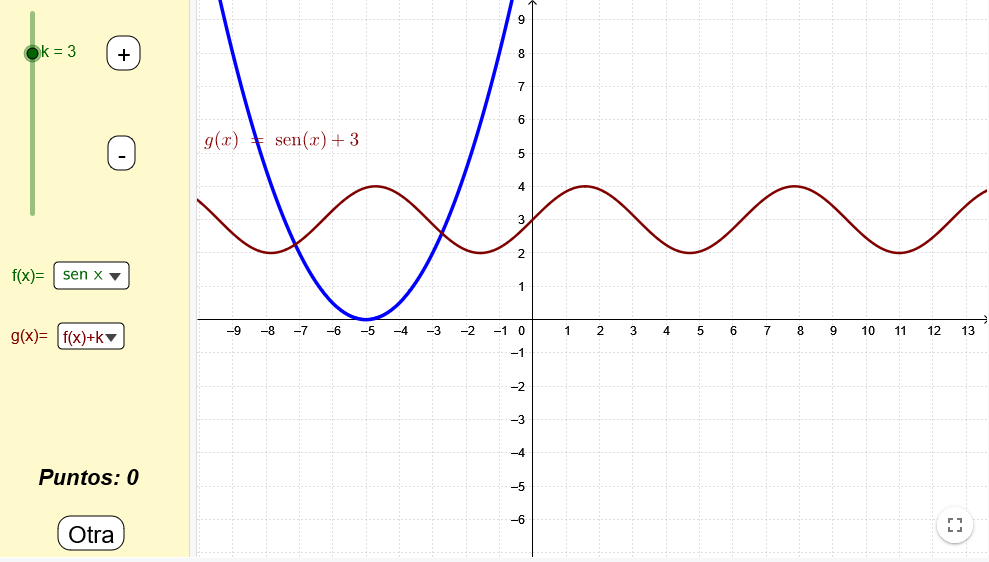
Prueba tu habilidad (transformando funciones)
En una pantalla aparecen dos funciones y hay que conseguir que coincidan eligiendo entre diferentes familias de funciones y jugando con los parámetros.
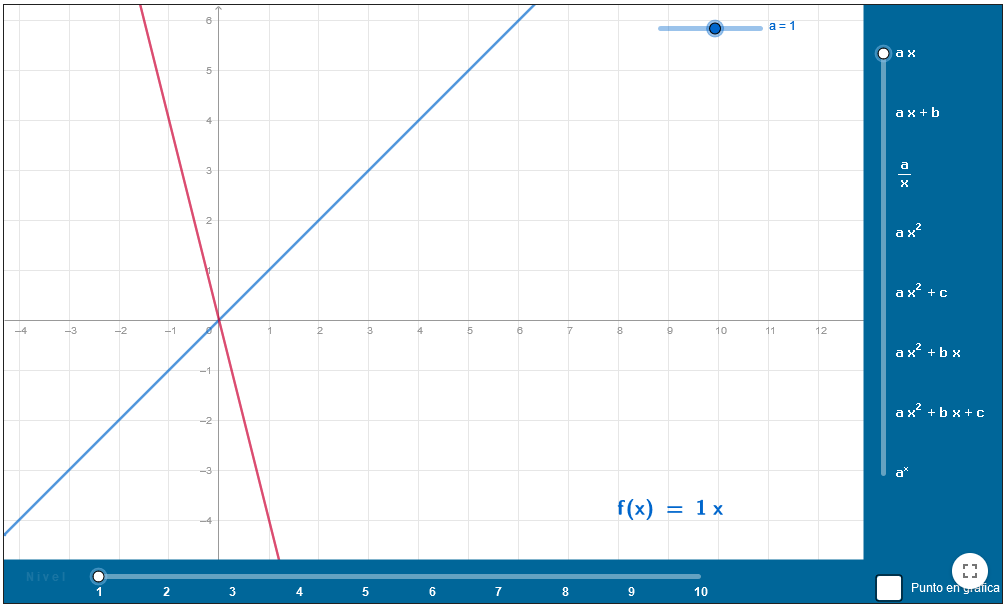
El juego de las funciones
Juego que permite asociar gráficas de funciones elementales con su ecuación. Hay que elegir la familia de funciones adecuada y mover los deslizadores hasta hallar los parámetros.
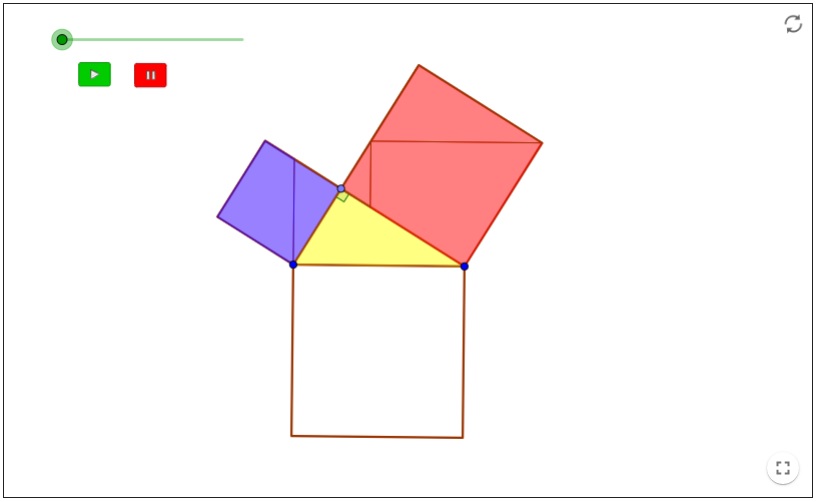
Teorema de Pitágoras. Demostración de Anaricio-Göpel
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. Las superficies que abarcan los cuadrados sobre los catetos se desplazan hasta completar la superficie del cuadrado sobre la hipotenusa, para lo que se descomponen en triángulos y cuadriláteros.
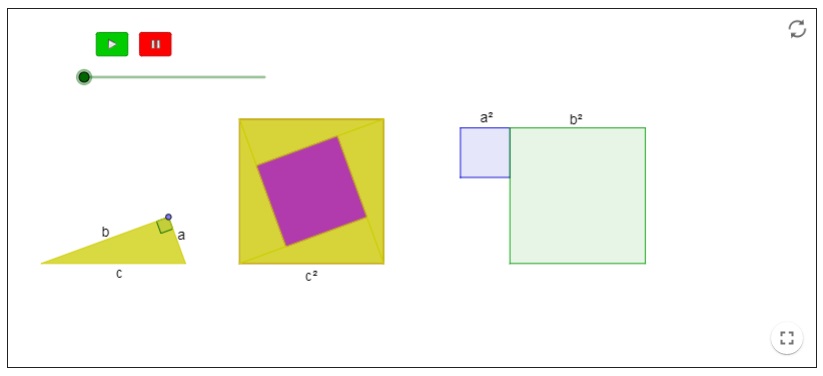
Teorema de Pitágoras. Demostración de Bhaskara
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. La superficie que abarca el cuadrado sobre la hipotenusa se desplaza hasta rellenar la suma de las superficies de los cuadrados sobre los catetos.
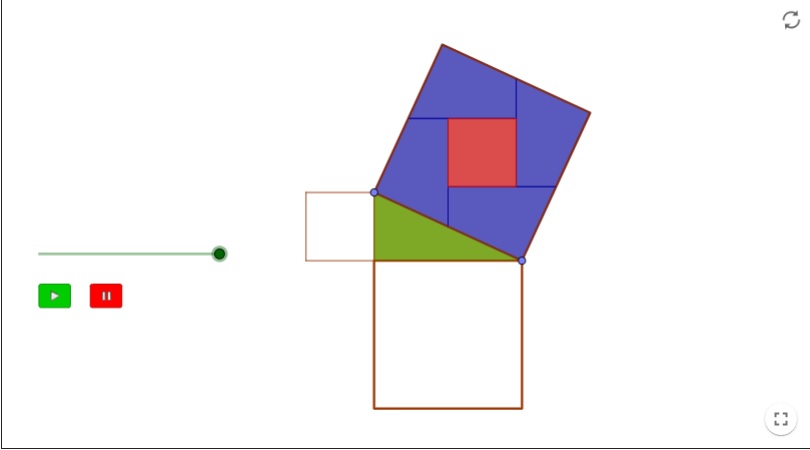
Teorema de Pitágoras. Demostración de Perigal
El recurso hace una demostración visual del Teorema de Pitágoras. El cuadrado sobre el cateto mayor se descompone en 4 cuadriláteros que se desplazan hasta el cuadrado sobre la hipotenusa. La superficie restante es la del cuadrado sobre el cateto pequeño.