Buscador global
Mostrando del 151 al 160 de 302 resultados filtrando por: Ciencias
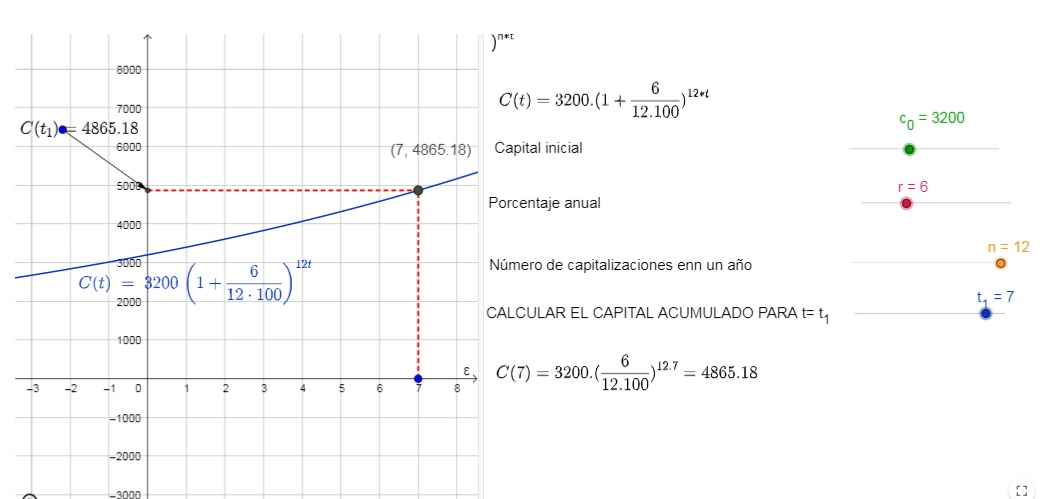
Interés compuesto y las funciones exponenciales asociadas
En el applet hay que introducir mediante deslizadores, el capital inicial (C_0), el tipo de interés (r), el tiempo considerado (t_1) y el número de capitalizaciones anuales (n). Se halla de forma automática el capital final (C_t) y se representa la función exponencial correspondiente.

Anualidades de capitalización
El applet resuelve de forma automática varios problemas de anualidades, en los que la fórmula de la suma de progresiones geométricas es fundamental. La resolución de problemas mediante pistas facilita la comprensión. Los problemas son autocorregibles y el applet asigna una puntuación dependiendo de las pistas utilizadas.
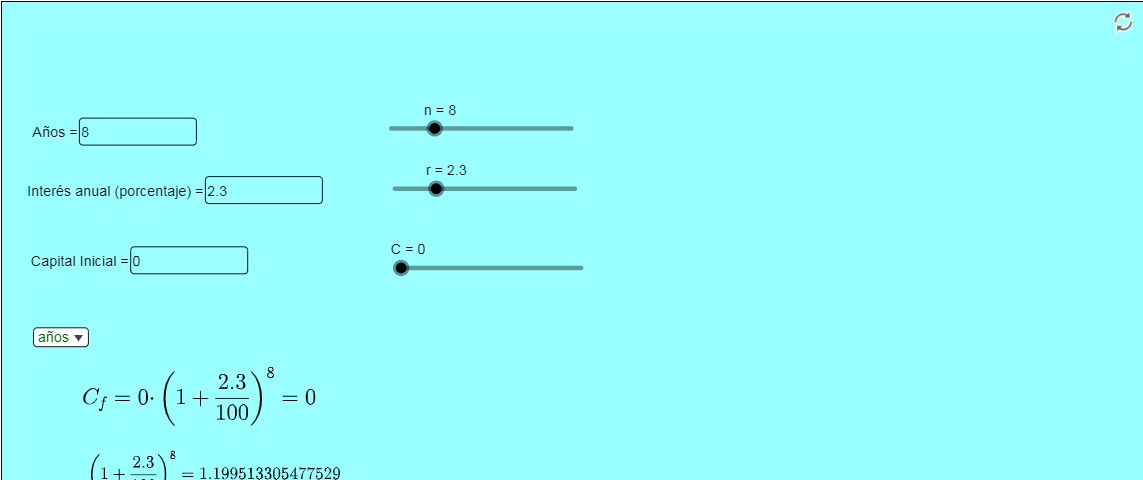
Calculadora de interés compuesto
El applet es una auténtica calculadora de interés compuesto. Hay que introducir mediante casillas de entrada o deslizadores, el capital inicial, el tipo de interés y los años que se consideren. Además se puede elegir la capitalización: anual, mensual, diaria, por horas, minutos o segundos. La fórmula se adapta y tenemos el resultado final.
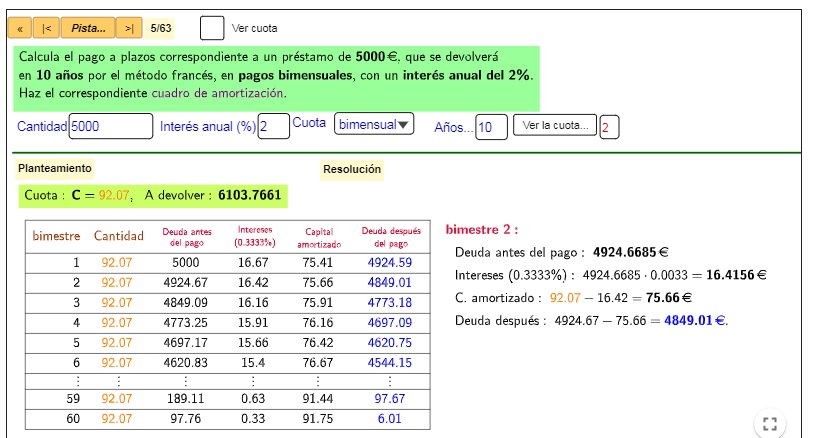
Amortización de préstamos
El applet resuelve de forma automática la cuota que tenemos que pagar para amortizar un préstamo. Mediante casillas de entrada hemos de introducir la cantidad total a devolver, el tipo de interés anual, la periodicidad y el número de años. La resolución mediante pistas facilita la comprensión. Los problemas son autocorregibles y el applet asigna una puntuación dependiendo de las pistas utilizadas.
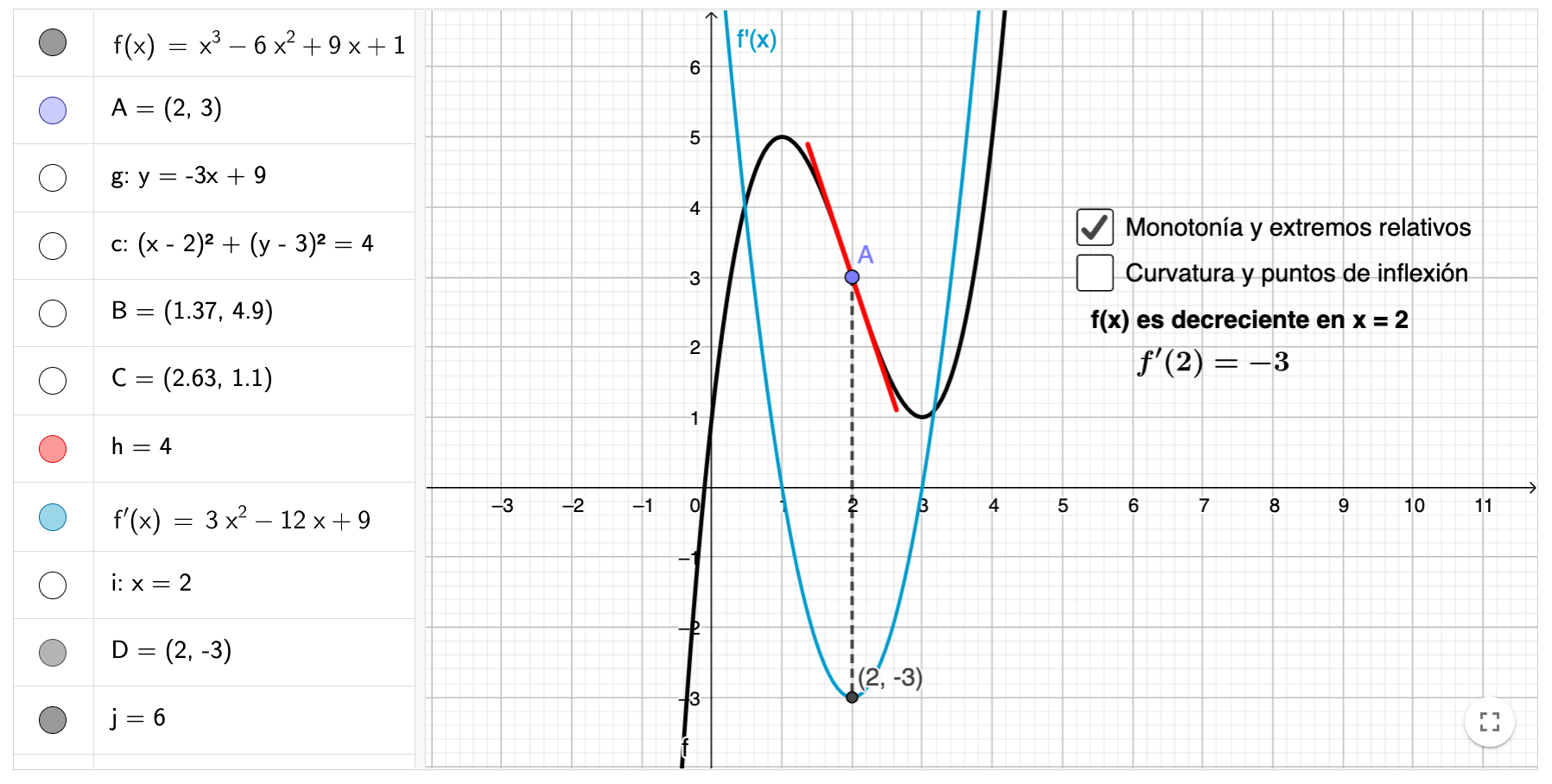
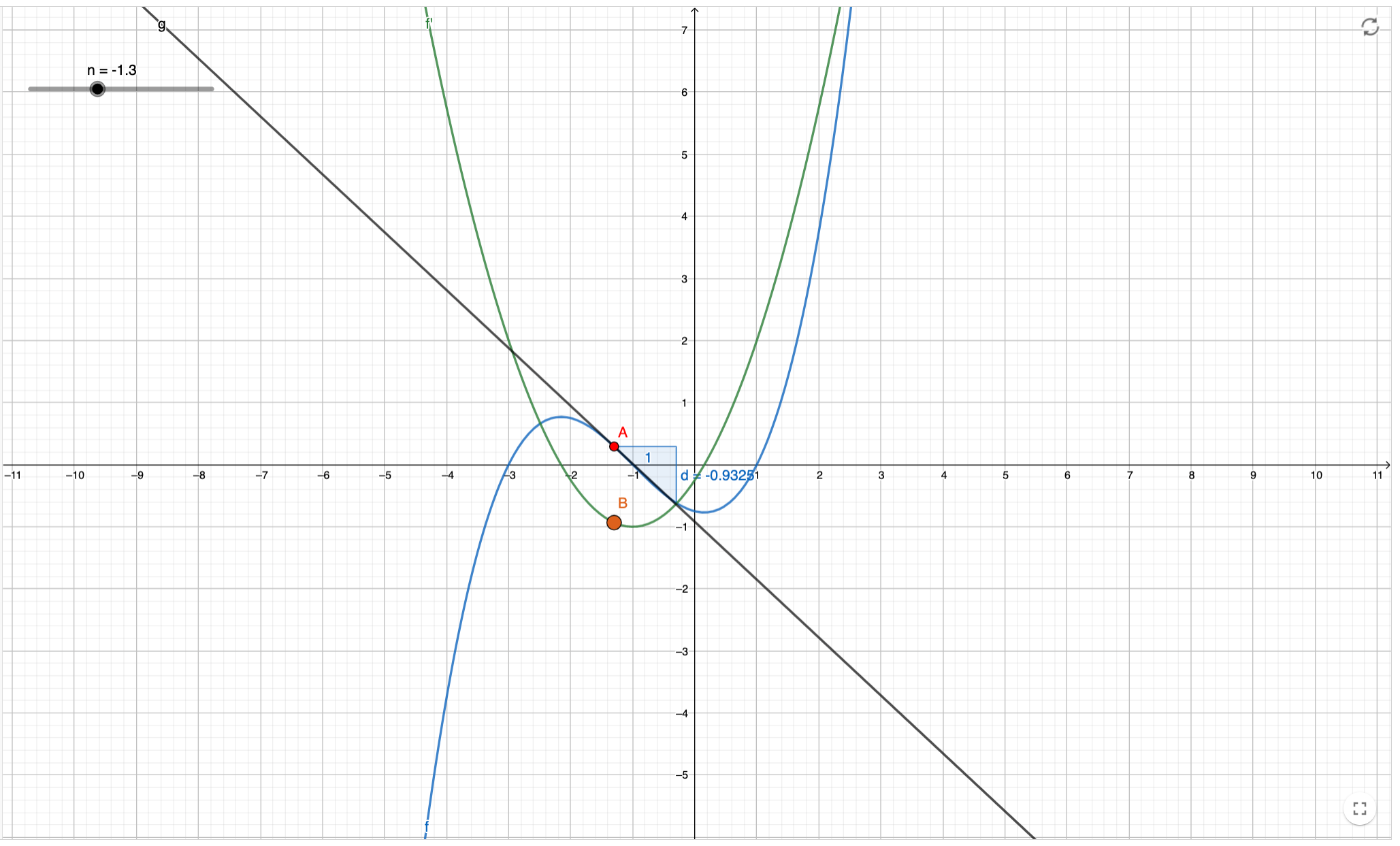
Monotonía y curvatura a partir de las derivadas
Con este recurso se puede visualizar la relación entre el valor de la derivada de función y su monotonía o la existencia de extremos relativos, así como entre el valor de la segunda derivada y su curvatura o la existencia de puntos de inflexión.
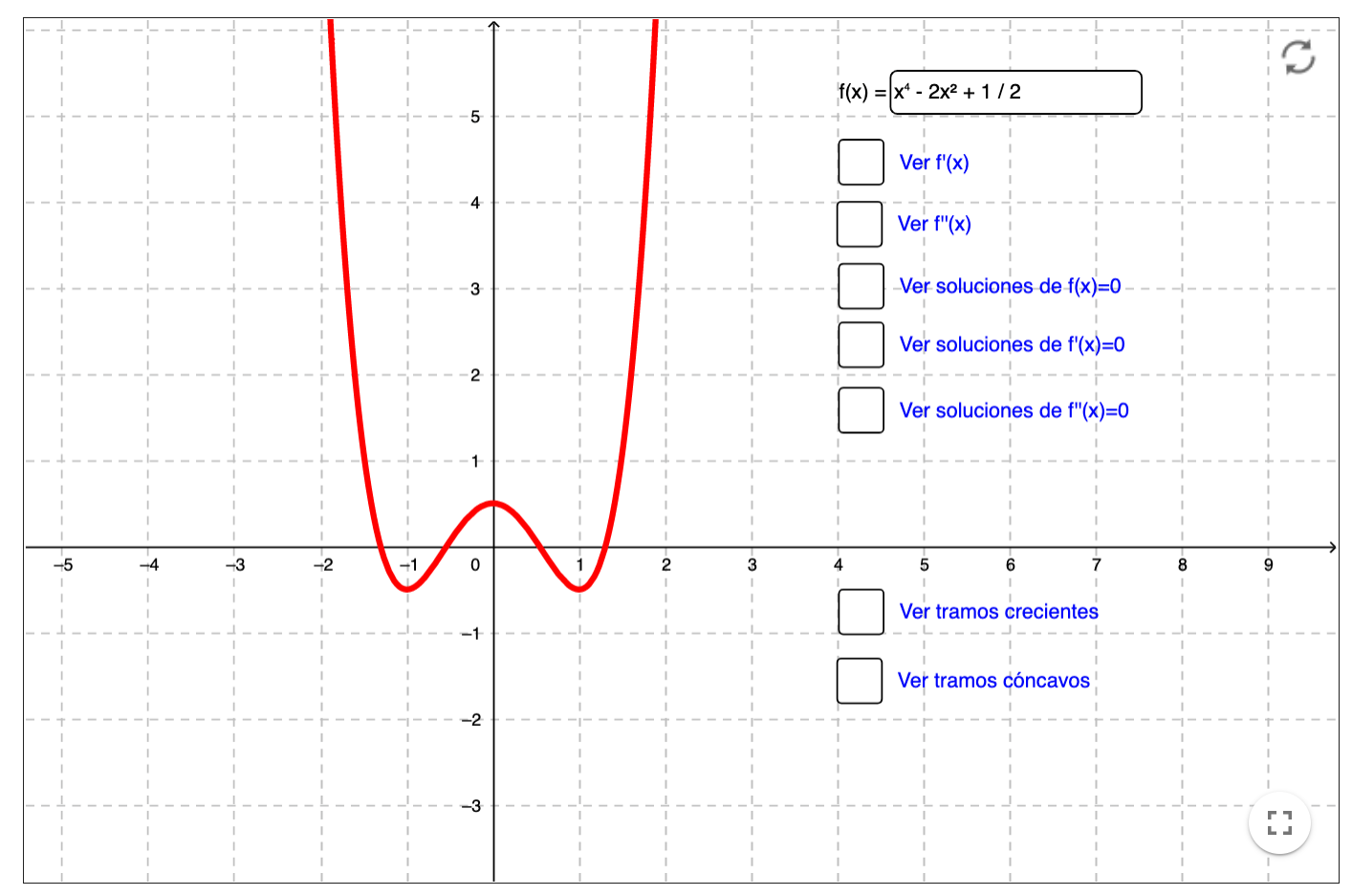
Monotonía y curvatura de una función
A partir de una función se puede visualizar la primera y segunda derivada, la monotonía, los extremos relativos, la curvatura y los puntos de inflexión.
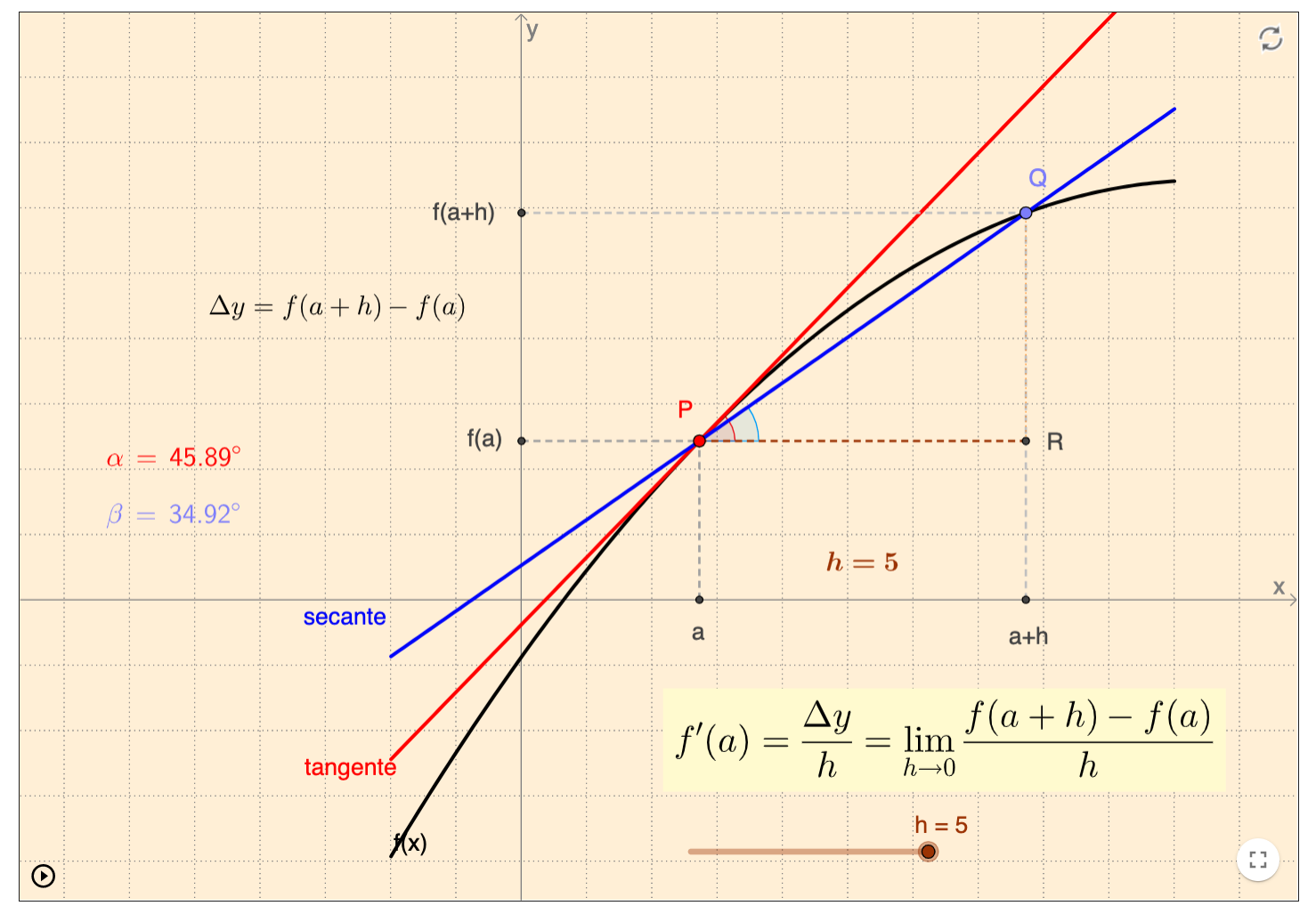
Derivada de una función en un punto
Con este recurso se puede visualizar el concepto de derivada como el límite de la tasa de variación media cuando la longitud del intervalo tiende hacia 0 relacionando dichos conceptos con las rectas tangente y secante, respectivamente.