Buscador global
Mostrando del 141 al 150 de 299 resultados filtrando por: Ciencias
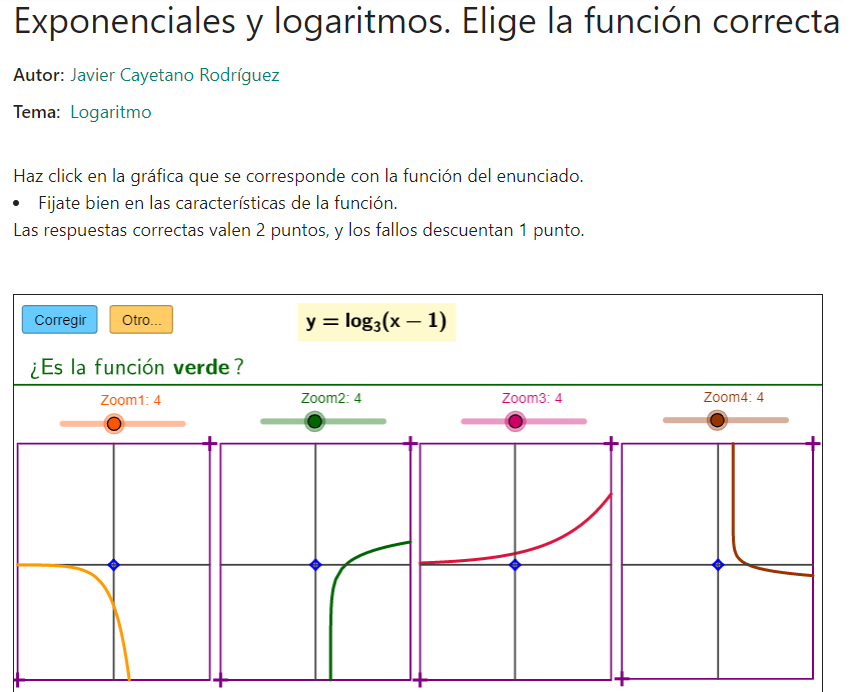
Exponenciales y logaritmos. Elige la función correcta
Se proporciona la expresión de una función y hay que elegir la gráfica correspondiente.
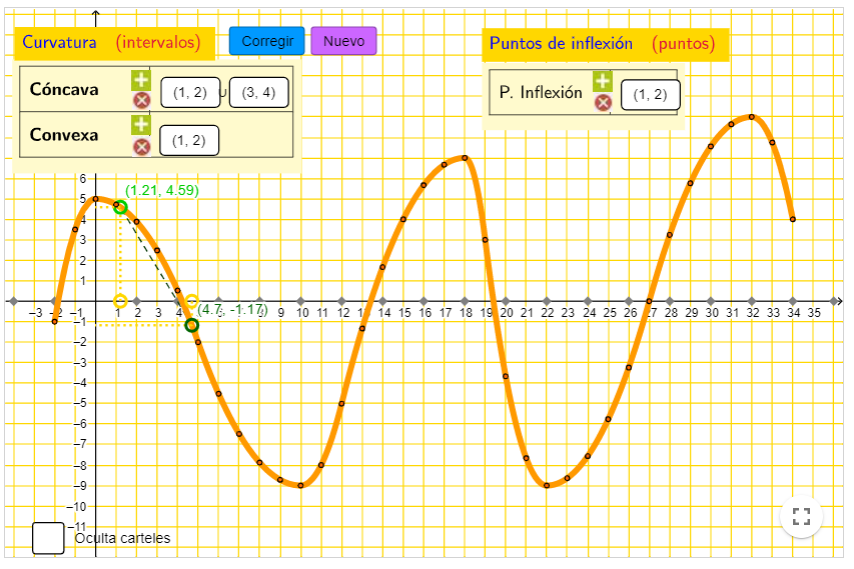
Curvatura(cóncava/convexa) e Inflexión
A partir de la gráfica de una función, hay que describir los intervalos de curvatura y los puntos de inflexión.

Ecuaciones de tercer grado
Resuelve ecuaciones de tercer grado paso a paso: cálculo de los divisores del término independiente, división del polinomio por la regla de Ruffini, resolución de la ecuación de segundo grado obtenida.

Producto de Matrices
El applet detalla, a través de ejemplos aleatorios cómo se hace el producto de dos matrices. El alumnado va eligiendo la fila de la primera matriz (i) y la columna de la segunda (j), para obtener el elemento (i,j) de la matriz producto. El grafo ayuda a que el algoritmo sea aprendido.

Método de Gauss – Resuelto
El applet repasa la resolución de sistemas utilizando el Método de Gauss. Presenta, en cada fase, 3 sistemas resueltos, uno con las 3 incógnitas despejadas, otro triangular y otro general, que ilustran perfectamente la rutina del método.

Inverse Matrix
El applet repasa el cálculo de la matriz inversa, especificando todo los pasos: cálculo del determinante, cálculo de la matriz adjunta, de la adjunta traspuesta, y al final, de la inversa. Introducimos la matriz por sus elementos y salen los cálculos de forma ordenada.
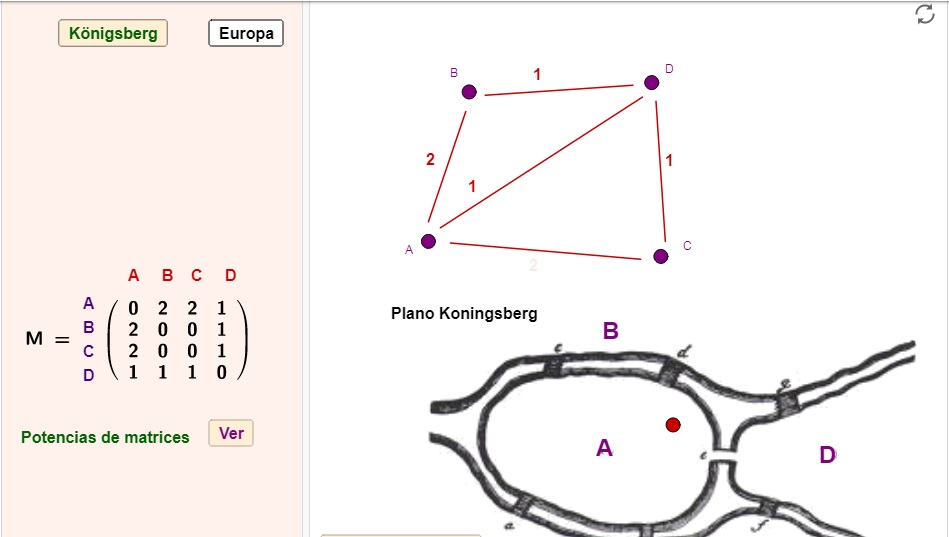
Matrices de conexiones
El applet presenta el conocido problema de los puentes de Königsberg, resuelto por Leonhard Euler en 1736 y cuya resolución dio origen a la teoría de grafos. Se plantea una matriz (M) que indica el número de puentes que es posible cruzar para pasar de un sector a otro. Se pide la interpretación de las potencias de M y resolver el problema inicial: ¿Hay un recorrido para cruzar a pie toda la ciudad, pasando por todos los puentes pero sólo una vez por cada uno?

Ecuaciones matriciales
El applet resuelve un buen abanico de ecuaciones con matrices. Para cada terna de matrices, propone 6 ecuaciones distintas que se resuelven paso a paso mediante el botón "Solución". Podemos variar las matrices de partida mediante el botón "Nuevo".
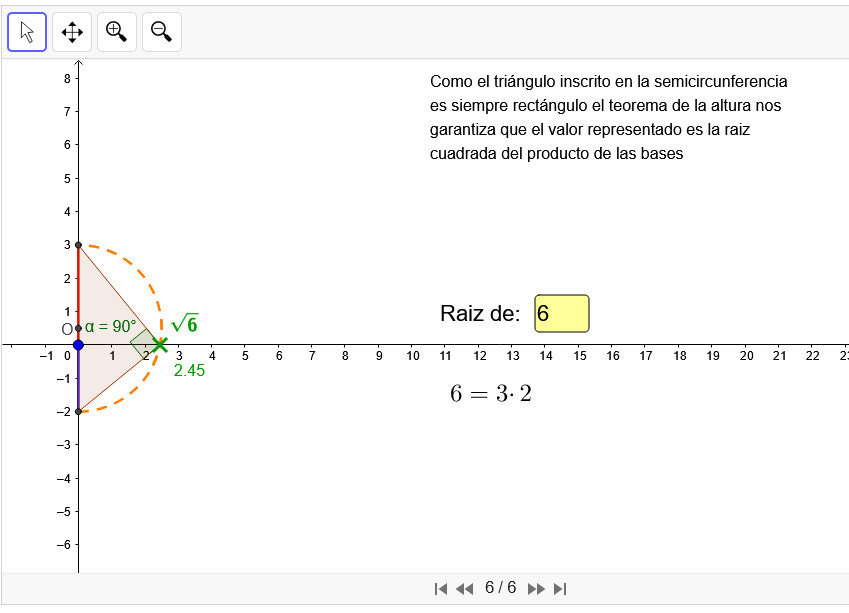
Representación de una raíz cuadrada en la recta real
Applet que explica, paso a paso, un método para representar raíces cuadradas irracionales en la recta real.

Vectores y matrices
El applet muestra la equivalencia entre las combinaciones lineales de vectores de R^3 y el rango de la matriz cuadrada de orden 3 correspondiente. Los 3 deslizadores son los coeficientes de la combinación lineal y vemos que x_1 u+x_2 v+x_3 w siempre coincide con la operación matricial A x.