Buscador global
Mostrando del 41 al 50 de 185 resultados filtrando por: 1º E.S.O.
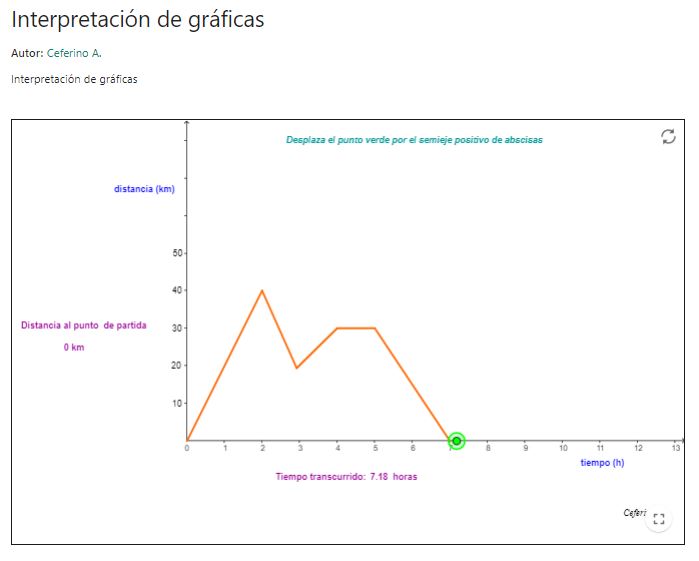
Interpretación de gráficas
Se presenta un gráfico en un diagrama cartesiano y un punto que se desliza sobre el trazo del gráfico que relaciona la distancia recorrida en kilómetros y el tiempo en horas que realiza un ciclista en su recorrido. El recurso es para explorar e iniciarse en la interpretación de gráficos.
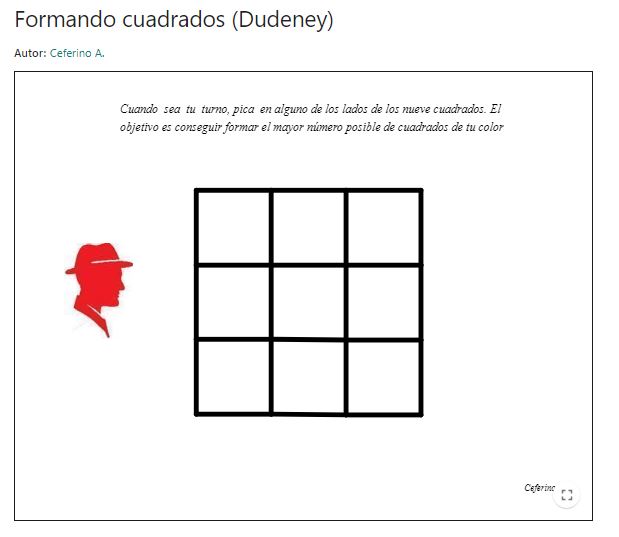
Formando cuadrados (Dudeney)
Se presenta un juego para dos personas jugadoras, donde en cada turno sobre una cuadrícula de 3x3 se tienen que ir eligiendo lados (que se van marcando en colores distintos según la persona jugadora) para realizar un cuadrado. El objetivo es conseguir formar el mayor número de cuadrados posibles teniendo en cuenta que se identifica el cuadrado para la persona jugadora que realice el cierre de dicho cuadrado.
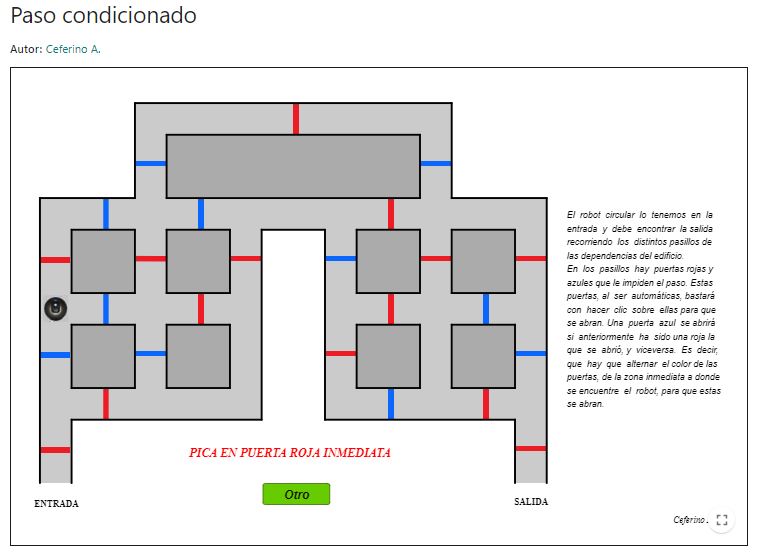
Paso condicionado
Se presenta la simulación del recorrido que debe hacer un robot por una serie de pasillos donde hay puertas rojas y azules (simuladas como líneas de estos colores). El robot que está en la entrada, debe llegar a la salida recorriendo los pasillos de tal forma que debe pasar por las puertas, que son automáticas (con un clic sobre ellas ya se deslizan para abrir) con la condición de que una puerta azul se abrirá si anteriormente ha sido una roja la que se abrió, y viceversa, es decir, una puerta roja se abrirá siempre y cuando se abrió anteriormente una azul. Hay que alternar el color de las puertas de la zona inmediata a donde se encuentre el robot para que se abran las puertas.

Múltiplos de un número 2 (Actividad)
Este applet muestra cuatro números de cuatro cifras y tienes que seleccionar cuál o cuáles de ellos son múltiplos del número, del 2 al 10, seleccionado en la parte izquierda del mismo.
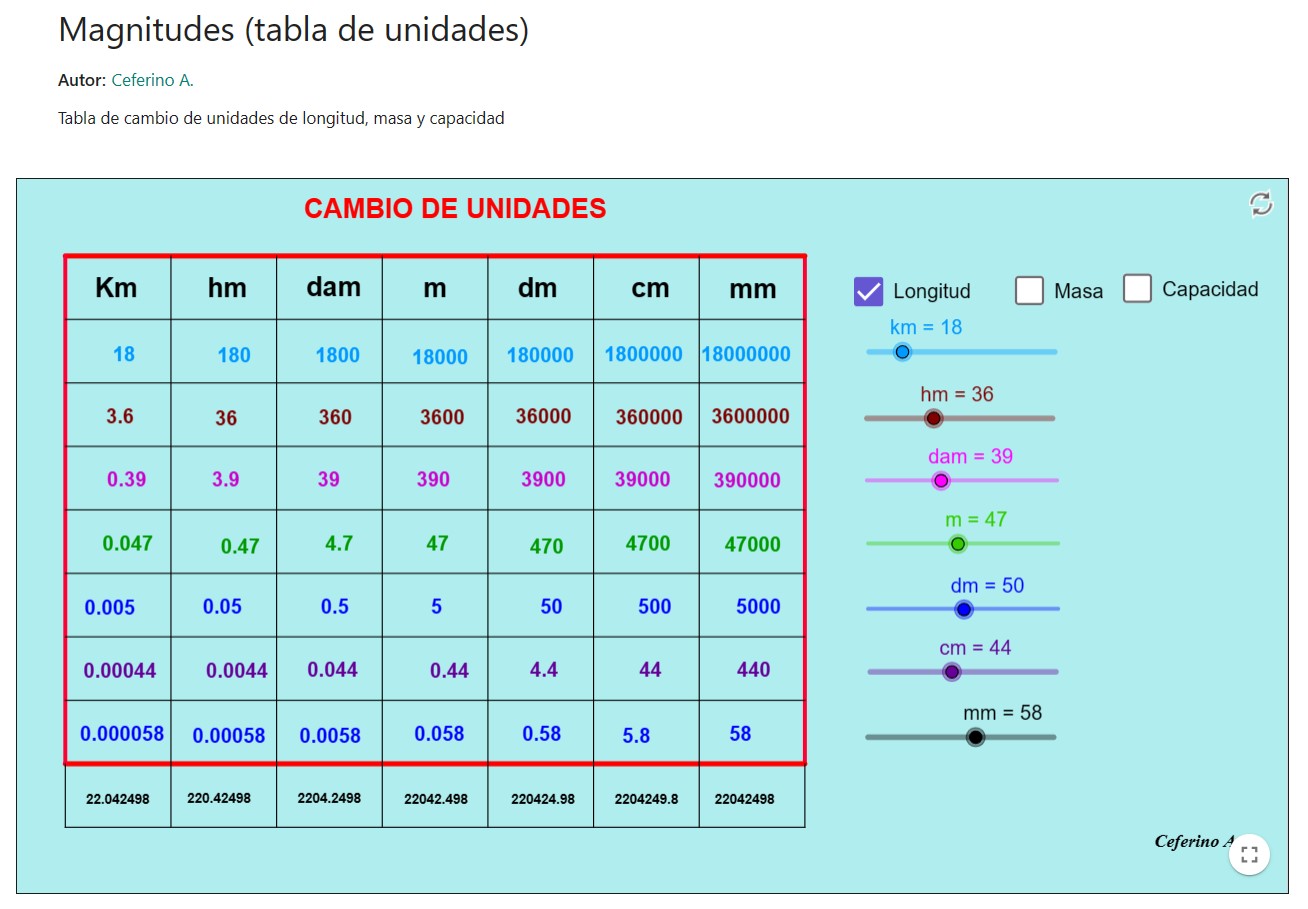
Magnitudes (tabla de unidades)
En este applet se muestra una "calculadora" para comprobar equivalencias entre cantidades de medida de longitud, masa y capacidad expresadas en diferentes órdenes de magnitud.
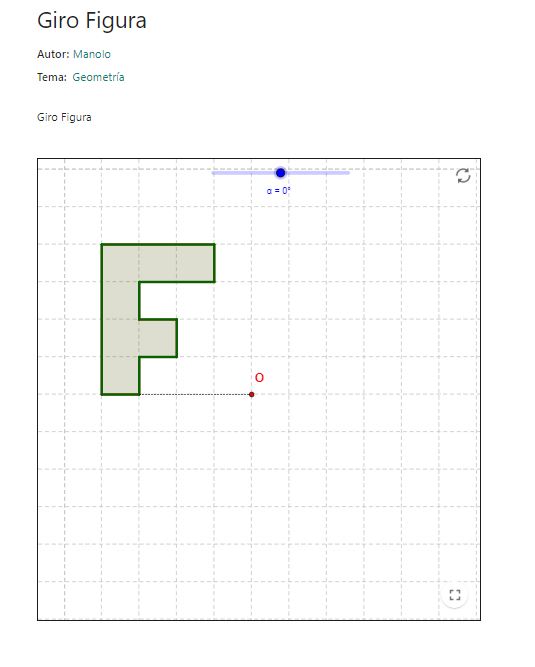
Giro Figura
Se presenta el giro de una figura plana que representa la letra F, sobre una cuadrícula, donde con un deslizador se puede modificar la amplitud de giro y donde también se muestra el centro de giro indicado con un punto rojo denominado O. Es un recurso ideal para explorar el giro o rotación de figuras planas y donde se puede ver de forma sencilla que al realizarse un giro, la figura cambia de posición y orientación, pero no se deforma: mantiene la longitud de sus lados y su área.
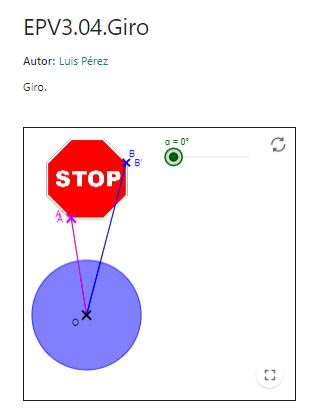
EPV3.04Giro
Se presenta el giro de una señal de stop, donde con un deslizador se puede modificar la amplitud de giro que se señala con el trazo superpuesto a un círculo y donde también se muestra el centro de giro, marcado como el centro del círculo que se traza con la amplitud del ángulo. Es un recurso ideal para explorar el giro o rotación de figuras planas.
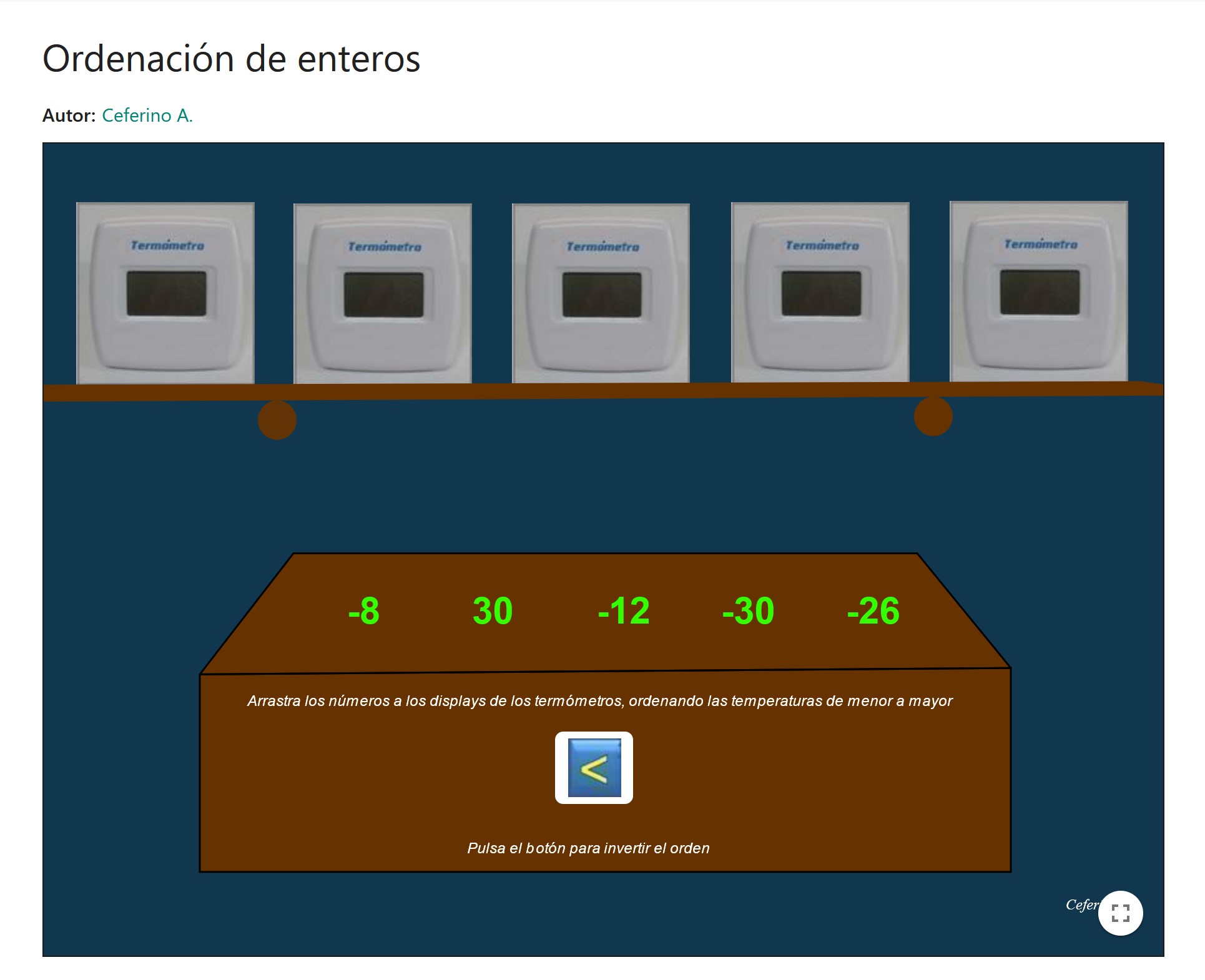
Ordenación de enteros
En el applet se muestra una situación con temperaturas de termómetros, y varios valores enteros (positivos y negativos). Hay que ordenar esos valores, bien de menor a mayor o bien de mayor a menor, según se elija.
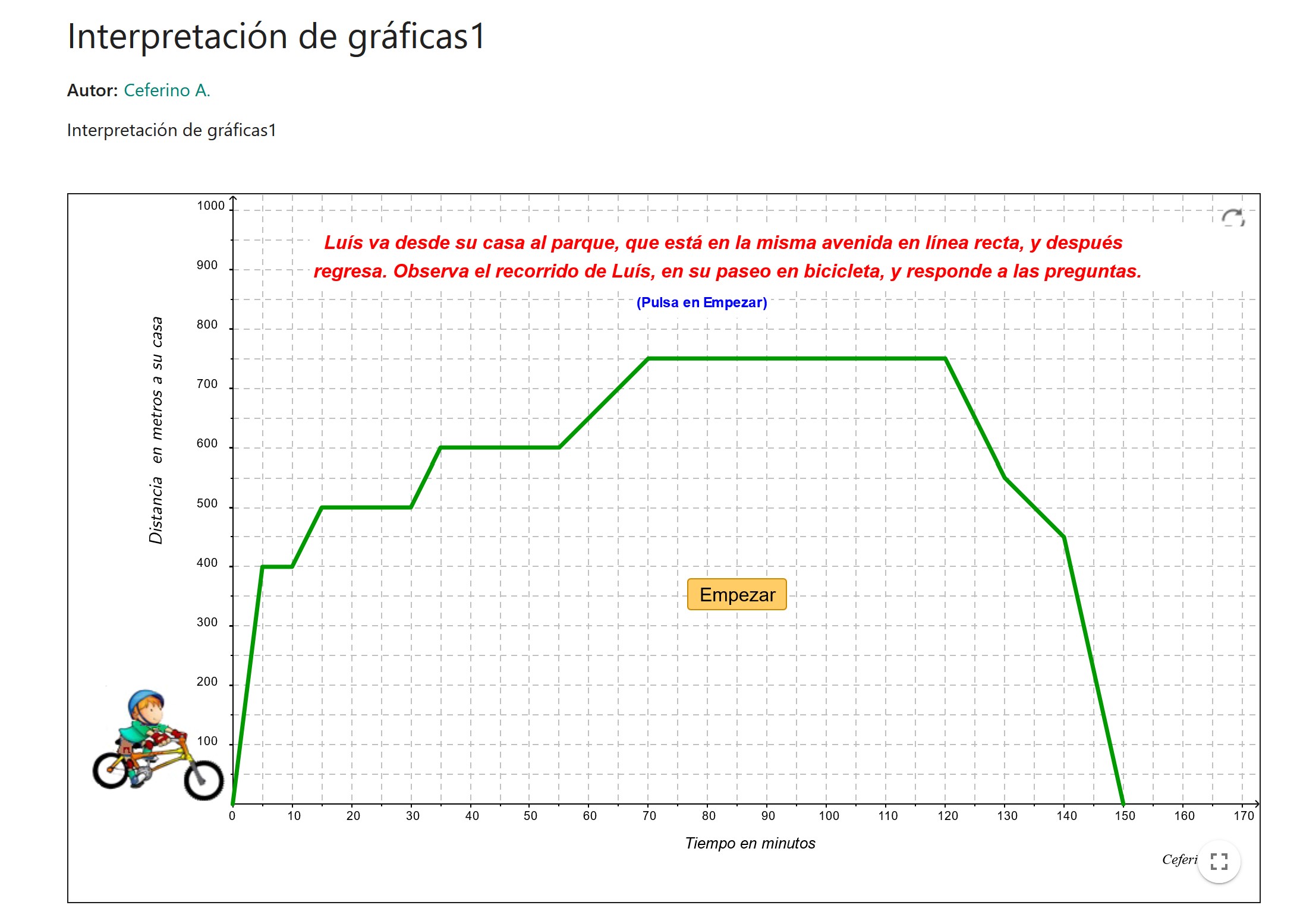
Interpretación de gráficos1
En el applet se presenta el gráfico tiempo - distancia de un paseo en bici, y se plantean diferentes preguntas vinculadas con la interpretación del gráfico y el movimiento que presenta (tiempos de movimiento, tiempos parados, distancias recorridas...)
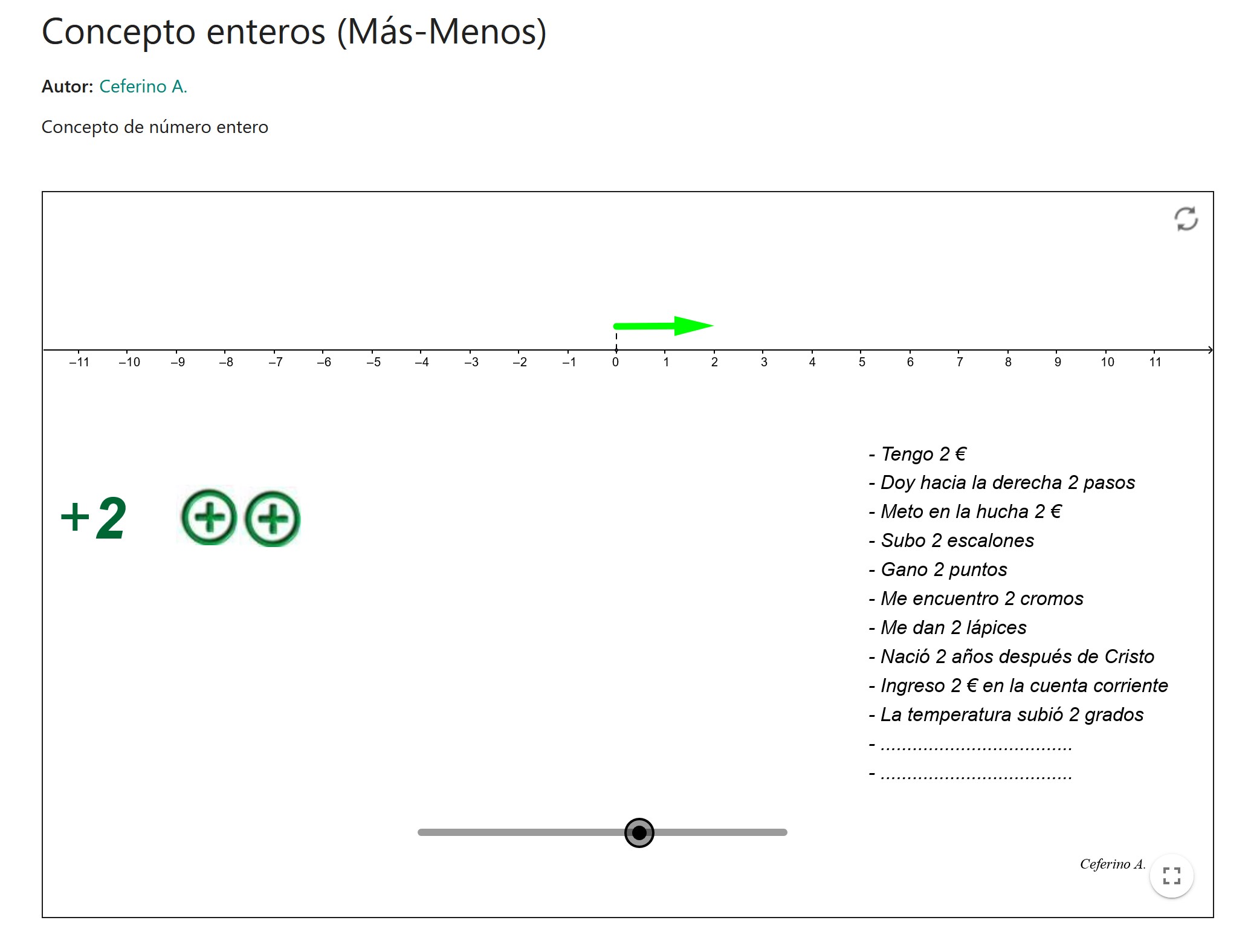
Concepto enteros (Más-Menos)
El applet puede usarse durante la introducción al concepto de número entero (positivo y negativo). Aparecen los números del -10 al 10, su representación con fichas positivas y negativas, en la recta numérica y un listado de frases de aplicación del número en situaciones reales.