Buscador global
Mostrando del 631 al 640 de 1392 resultados para: Nearpod: mucho más que una aplicación interactiva filtrando por: ESO
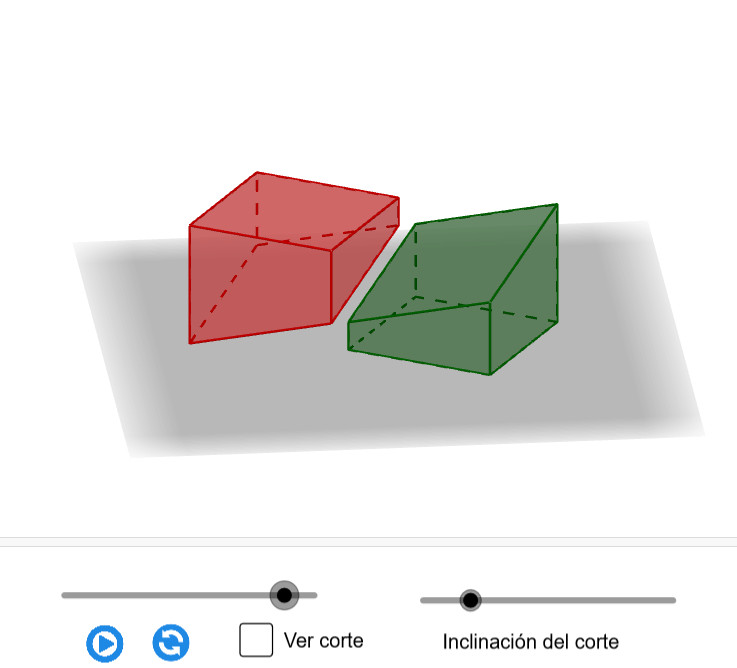
Mitad del cubo. Rombos
El applet muestra la sección que se produce en un cubo cuando lo cortamos con un plano que pasa por una de sus diagonales espaciales y los puntos medios de dos aristas opuestas dando lugar a un rombo. Se puede modificar la inclinación del corte para obtener otros polígonos.
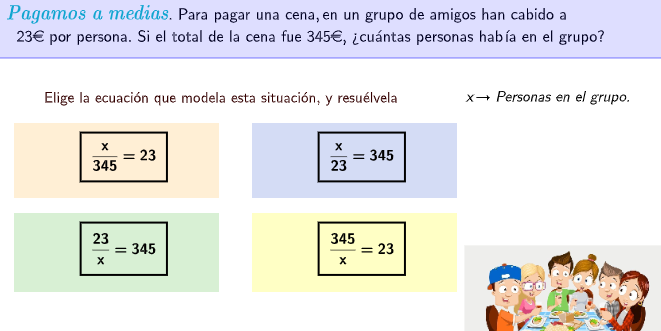
Traducir del lenguaje algebraico al cotidiano (y viceversa)
Se proponen problemas sencillos a los que hay que asociar una ecuación entre 4 posibles. El alumnado habrá de elegir la ecuación, resolverla e introducir el resultado en el applet. Se autocorregirá y se irán sumando puntos dependiendo del número de problemas modelado y resuelto de forma correcta.
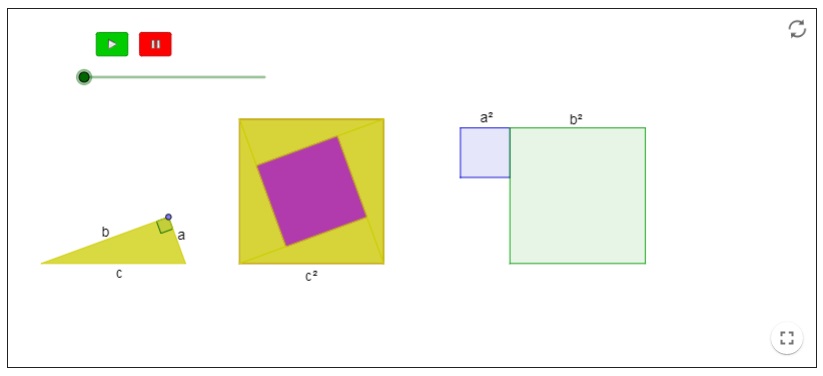
Teorema de Pitágoras. Demostración de Bhaskara
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. La superficie que abarca el cuadrado sobre la hipotenusa se desplaza hasta rellenar la suma de las superficies de los cuadrados sobre los catetos.
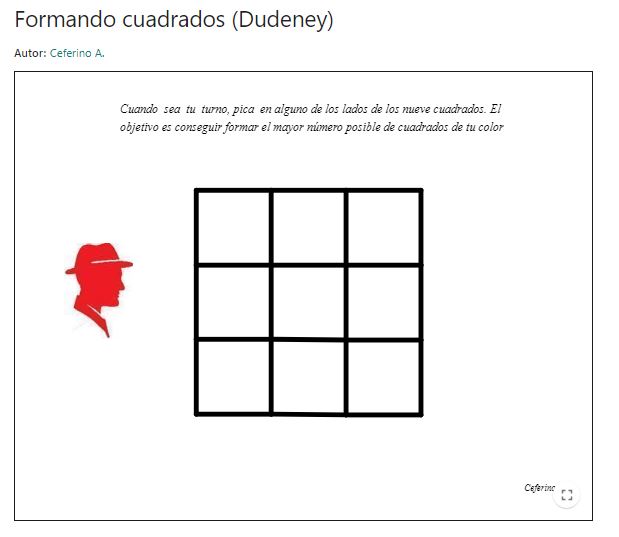
Formando cuadrados (Dudeney)
Se presenta un juego para dos personas jugadoras, donde en cada turno sobre una cuadrícula de 3x3 se tienen que ir eligiendo lados (que se van marcando en colores distintos según la persona jugadora) para realizar un cuadrado. El objetivo es conseguir formar el mayor número de cuadrados posibles teniendo en cuenta que se identifica el cuadrado para la persona jugadora que realice el cierre de dicho cuadrado.
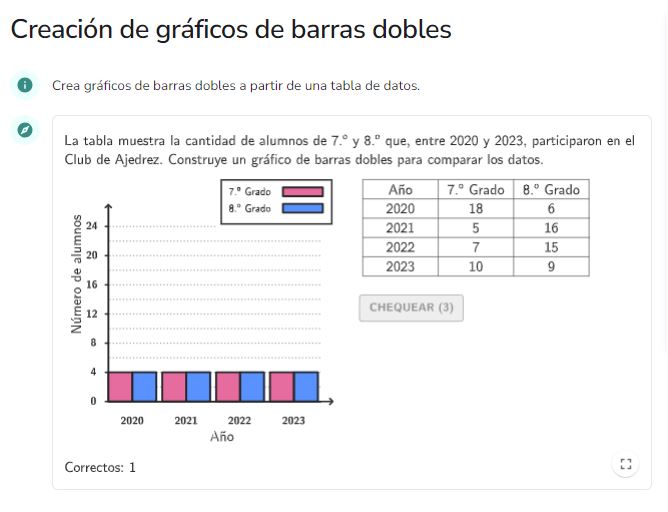
Creación de gráficos de barras dobles
El applet presenta una tabla de datos que se acompaña con un texto explicativo, para construir a partir de este contexto un diagrama de barras. El gráfico se presenta con sus ejes, simplemente hay que arrastrar las barras hasta la altura que debe reflejar los datos aportados por la tabla. Además el propio applet ofrece autocorrección (a través del botón "chequear").

Evolución de la Violencia a la Infancia en España según las víctimas (2009-2016)
Informe longitudinal sobre Evolución de la Violencia a la Infancia, en el que se analiza una muestra de 25.000 casos atendidos por el Teléfono ANAR, incluyendo el impacto de la tecnología en algunas problemáticas.
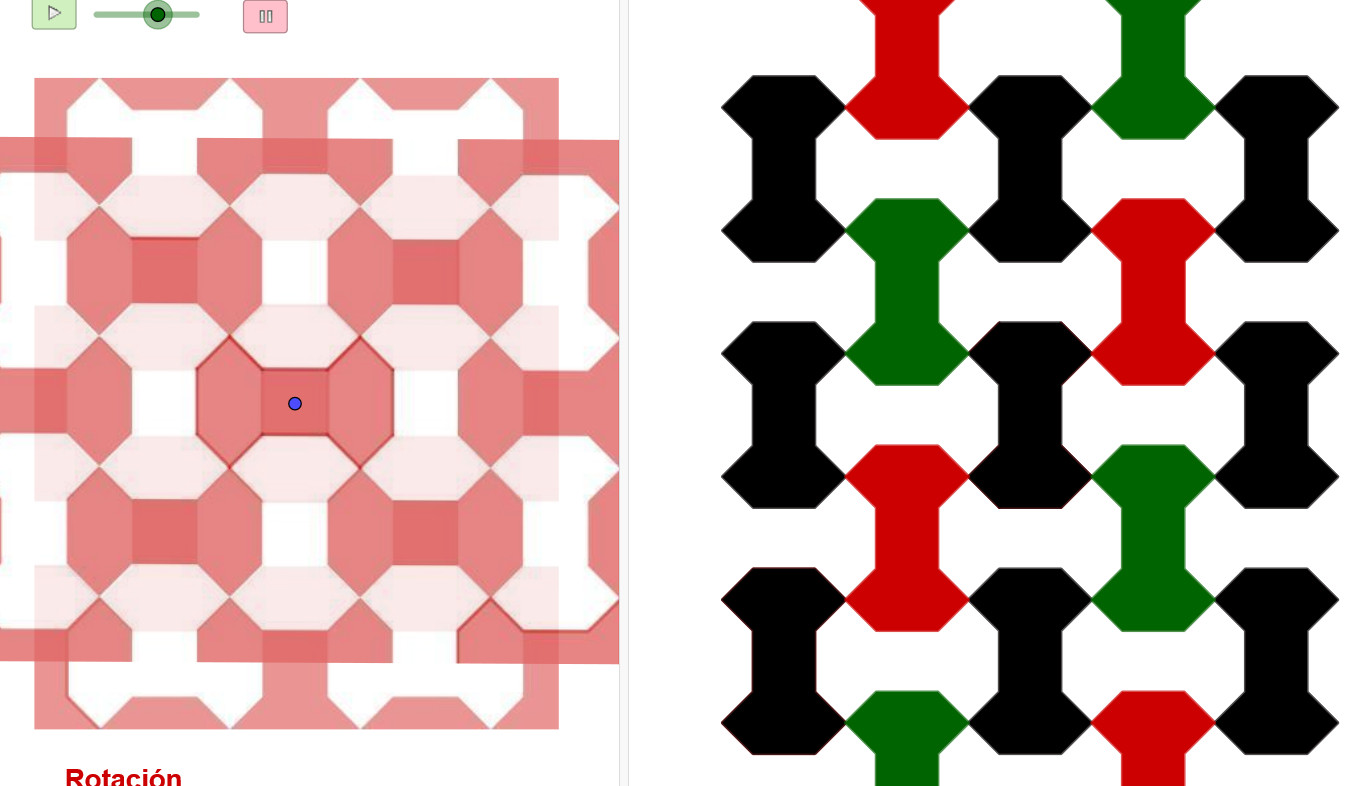
El hueso y los movimientos en un mosaico
Applet de Geogebra que presenta una secuencia animada para construir la baldosa del hueso, después con la baldosa se diseña el mosaico y se termina con el estudio de las simetrías de la composición.
Exploring our monuments
En esta actividad, el alumnado elegirá un monumento que tenga que ver con el patrimonio cultural de su localidad, región o provincia. Una vez que el monumento/s se haya seleccionado, se consultará en la web Europeana para conocerlo en profundidad. La labor de investigación conllevará dar respuesta a diferentes preguntas que se plantearán en pequeños grupos, trabajándose la técnica cooperativa “me convierto en experto”. La labor de investigación se completará con una visita al propio monumento, en la que pediremos al alumnado que eche un vistazo a la tienda de regalos que suele haber. Les pediremos que tomen nota de los objetos que hay, con la idea de poder debatir a posteriori sobre por qué la gente suele querer llevarse un recuerdo del lugar que visita. En clase se debatirá sobre qué otros objetos fomentan el patrimonio cultural de su país o región. El alumnado podrá, entonces, diseñar objetos a raíz de lo aprendido y enviarlos a sus socios. La información recopilada se recogerá en un muro colaborativo cuyo enlace se compartirá en el TwinSpace con los centros participantes.

Sistemas de dos ecuaciones lineales con dos incógnitas
El applet muestra qué es una ecuación lineal con dos incógnitas, indicando que tiene infinitas soluciones. Se definen los sistemas de dos ecuaciones lineales con dos incógnitas y se clasifican atendiendo al número de soluciones. La escena termina con ejercicios que evalúan si se saben clasificar los sistemas observando los coeficientes.

Dibujar la parábola a partir del vértice y un punto
Actividad en la que los alumnos deben colocar e ir moviendo el vértice y uno de los puntos de la parábola (el simétrico aparece al otro lado del eje) de una función cuadrática hasta conseguir que la parábola sea la gráfica de la función cuadrática cuya ecuación se daba como enunciado.