Buscador global
Mostrando del 11 al 20 de 41 resultados para: Nearpod: mucho más que una aplicación interactiva filtrando por: Triángulos
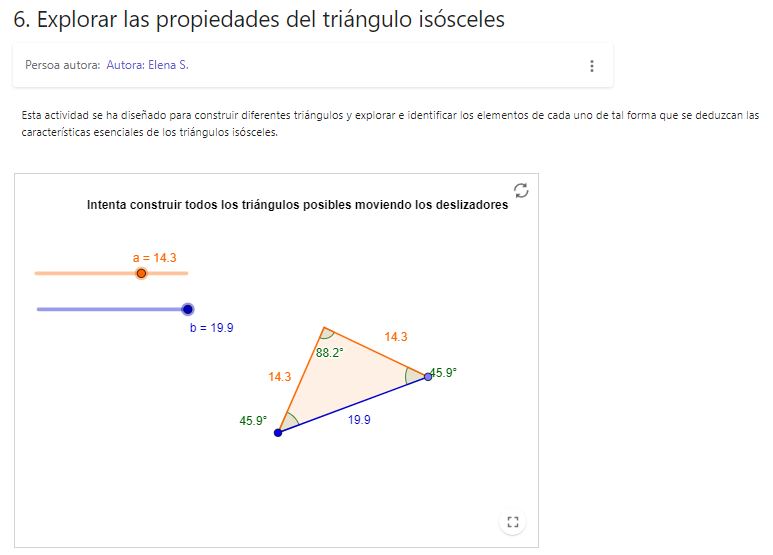
6. Explorar las propiedades del triángulo isósceles
El applet presenta la construcción de un triángulo isósceles y unos deslizadores que permiten cambiar la longitud de sus lados para explorar los diferentes triángulos que se pueden construir para deducir que todos tienen una cualidad en común que caracteriza a los triángulos isósceles: dos lados con la misma longitud y dos ángulos con la misma amplitud.
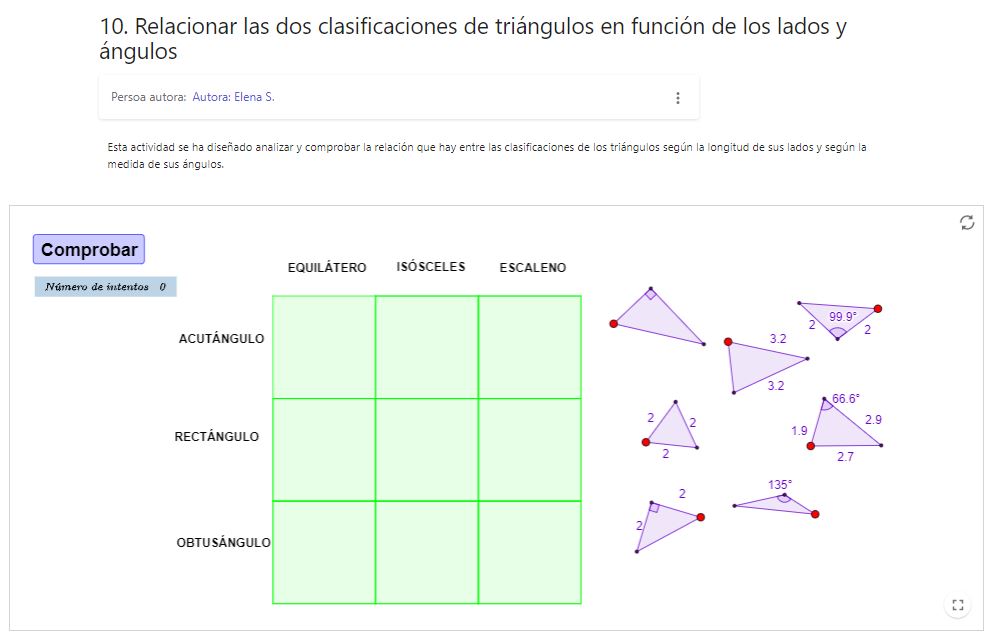
10. Relacionar las dos clasificaciones de triángulos en función de los lados y ángulos
El applet presenta una serie de triángulos que se deben clasificar en una tabla de doble entrada según las clasificaciones dadas las longitudes de sus lados como la amplitud de sus ángulos. Una vez realizada la clasificación se puede comprobar mediante el botón apareciendo la tabla pintada de verde o rojo para indicar si está correcta o no la colocación de los distintos triángulos.
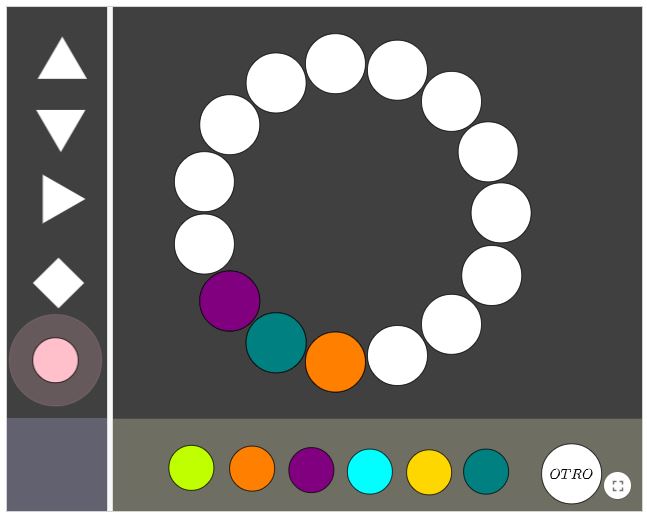
Figuras en serie
La actividad propone que se completen series de colores dentro de una figura cerrada. A la izquierda de la escena, se presentan, a una serie de figuras geométricas cerradas (triángulos, cuadrados y círculos), cuyo contorno está formado por el mismo tipo de figuras. La actividad permite seleccionar con cuál se quiere trabajar. Una vez elegida, se trata de continuar la serie a partir de los elementos coloreados que sirven como punto de partida. En el caso de los triángulos y el cuadrado, se muestra como patrón uno de los lados del perímetro y hay que completar los otros. En el caso del círculo los puntos coloreados aparecerán en distintas posiciones cuando se reinicie la actividad con el botón "OTRO".

Figuras planas: Triángulos
Applet de GeoGebra que presenta una clasificación de los triángulos según sus lados y ángulos. También muestra la definición y propiedades de los triángulos y la desigualdad triangular. Permite interacción.
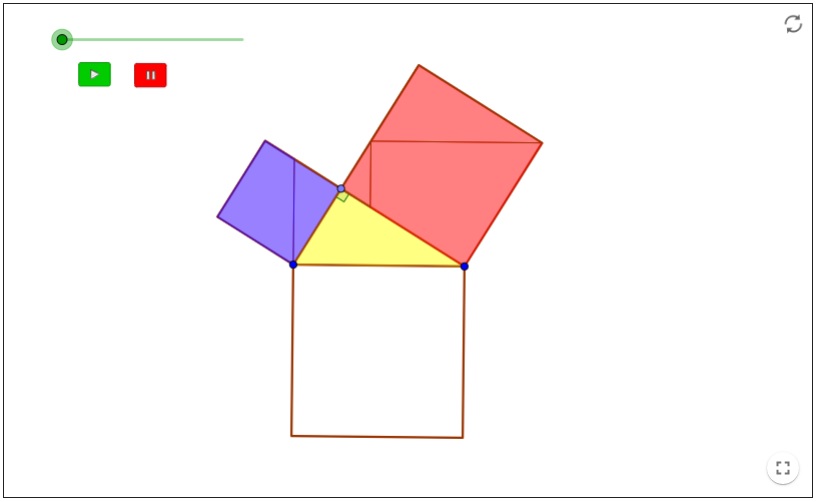
Teorema de Pitágoras. Demostración de Anaricio-Göpel
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. Las superficies que abarcan los cuadrados sobre los catetos se desplazan hasta completar la superficie del cuadrado sobre la hipotenusa, para lo que se descomponen en triángulos y cuadriláteros.
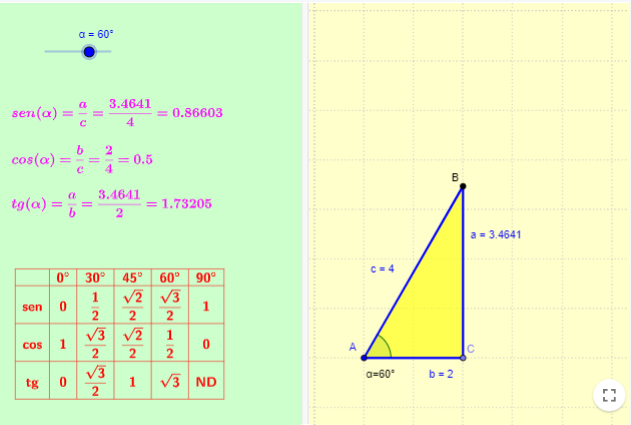
Razones trigonométricas de ángulos agudos
Applet de GeoGebra que presenta la definición de las razones trigonométricas de los ángulos agudos así como una tabla con el valor de las razones trigonométricas de los ángulos notables del primer cuadrante.
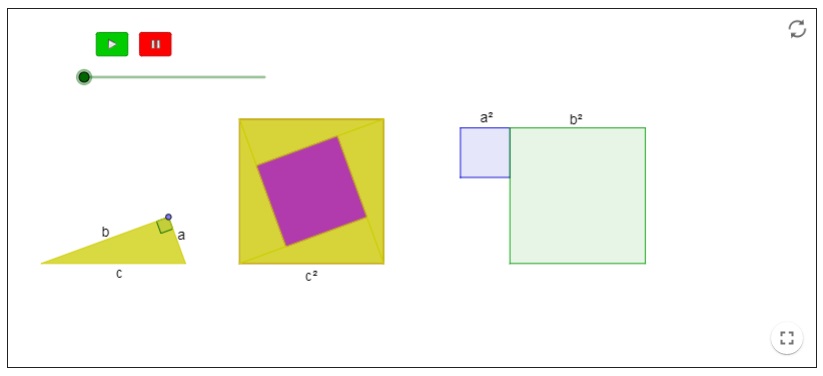
Teorema de Pitágoras. Demostración de Bhaskara
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. La superficie que abarca el cuadrado sobre la hipotenusa se desplaza hasta rellenar la suma de las superficies de los cuadrados sobre los catetos.
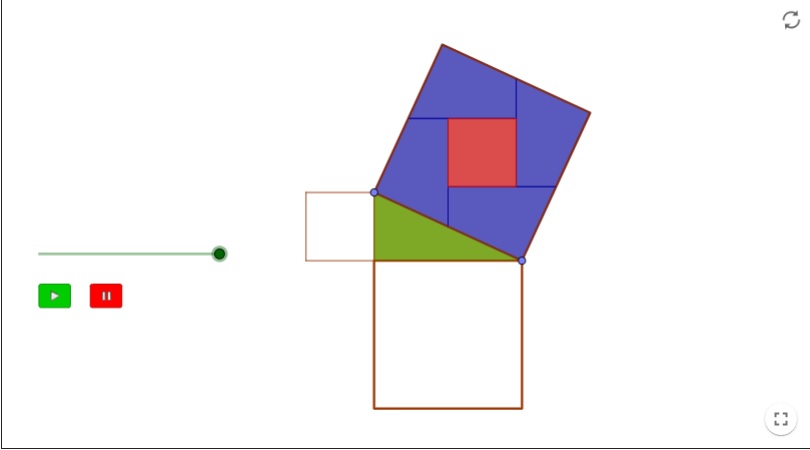
Teorema de Pitágoras. Demostración de Perigal
El recurso hace una demostración visual del Teorema de Pitágoras. El cuadrado sobre el cateto mayor se descompone en 4 cuadriláteros que se desplazan hasta el cuadrado sobre la hipotenusa. La superficie restante es la del cuadrado sobre el cateto pequeño.
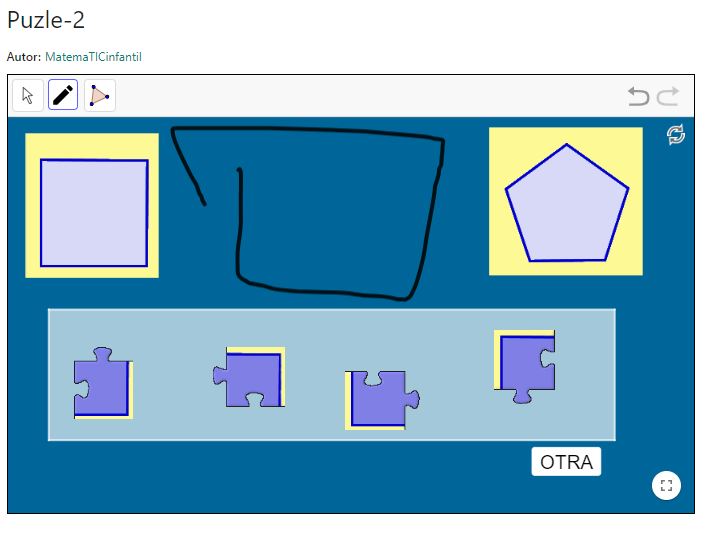
Puzle-2
Se presenta dos polígonos (elegidos aleatoriamente entre los cuatro que se trabajan, triángulo, cuadrado, pentágono y hexágono) y las piezas de uno de ellos, de modo que se debe montar el polígono sin saber si es uno u otro. Una vez construido se identifica el polígono y con la herramienta Lápiz o Polígono la pueden dibujar. Para borrar el dibujo es necesario actualizar el recurso.
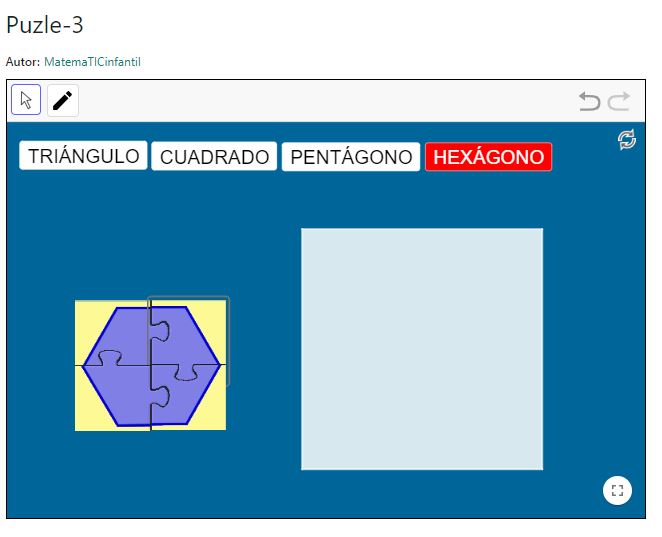
Puzle-3
Se presenta las palabras de los cuatro polígonos: triángulo, cuadrado, pentágono y hexágono. Eligiendo una de estas opciones aparece las piezas de un puzle para realizar dicha figura. Se puede también realizar su trazo o dibujo con ayuda de la herramienta Lápiz en un recuadro que ofrece el propio recurso, y luego mover el trazo y superponerlo a la figura, etc. Para borrarlo hay que actualizar el recurso.