Buscador global
Mostrando del 1 al 10 de 25 resultados para: Nearpod: mucho más que una aplicación interactiva filtrando por: InteractivoMedida y cambio
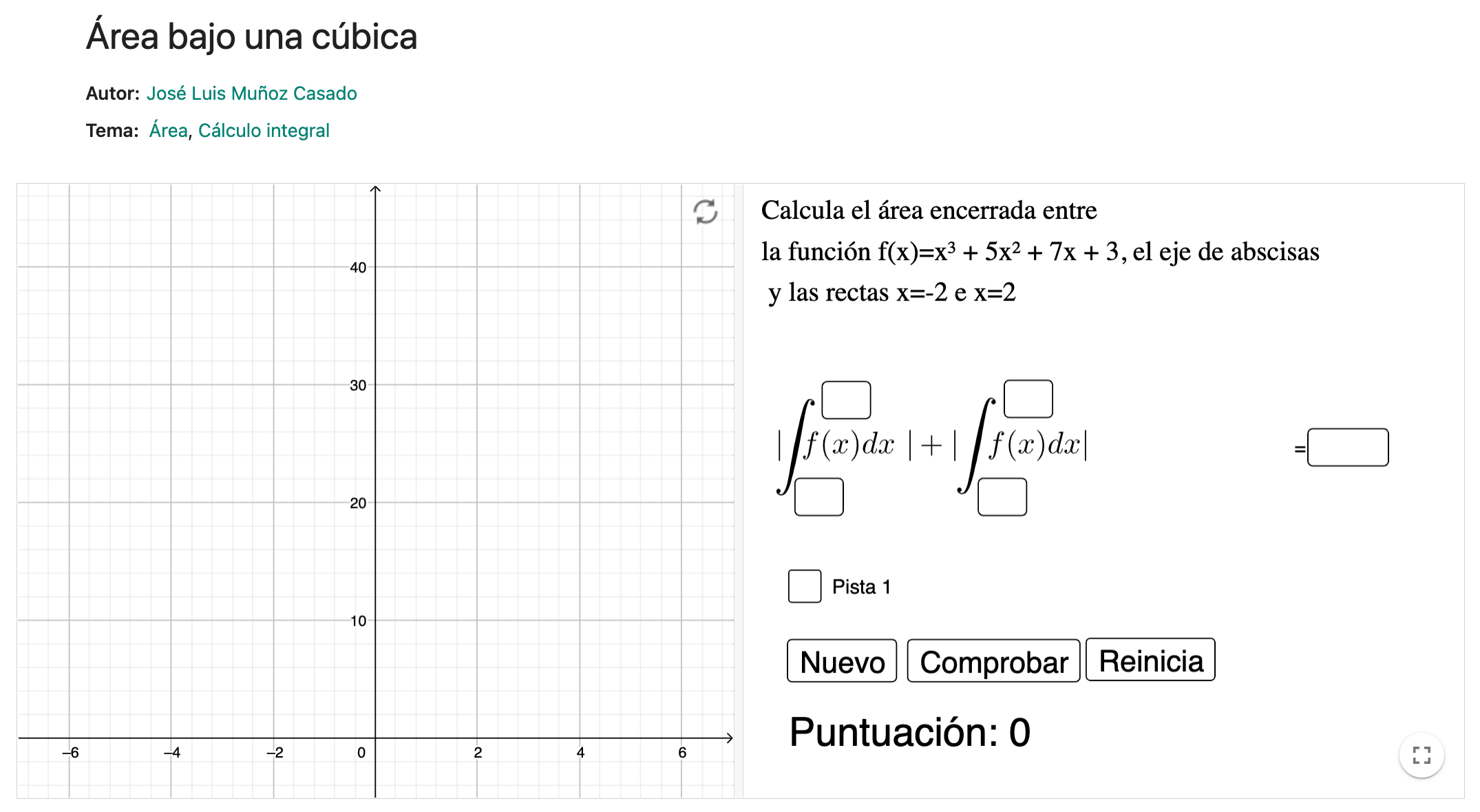
Área bajo una cúbica
Actividad autocorregible para practicar el cálculo de área bajo una cúbica.
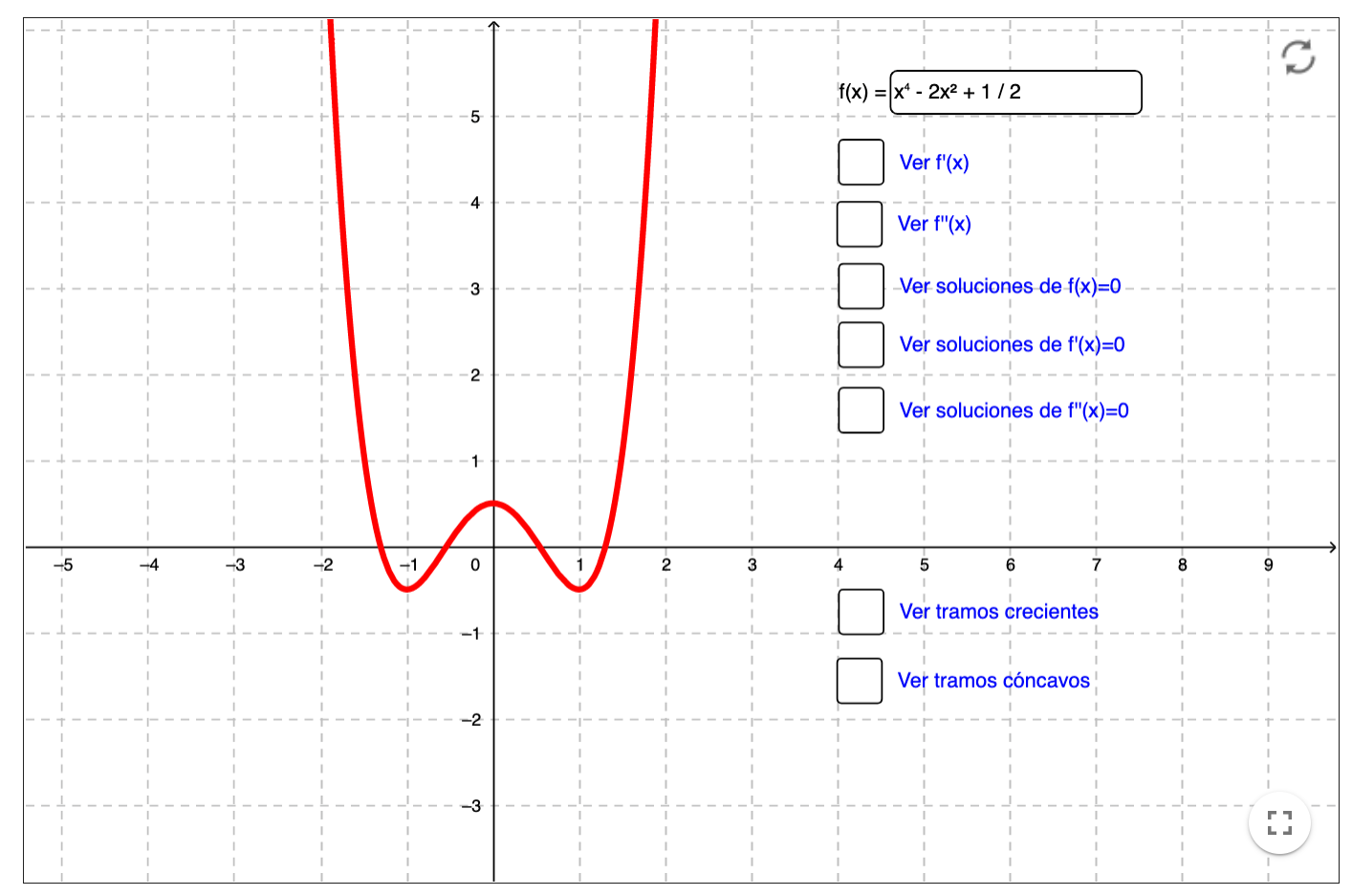
Monotonía y curvatura de una función
A partir de una función se puede visualizar la primera y segunda derivada, la monotonía, los extremos relativos, la curvatura y los puntos de inflexión.
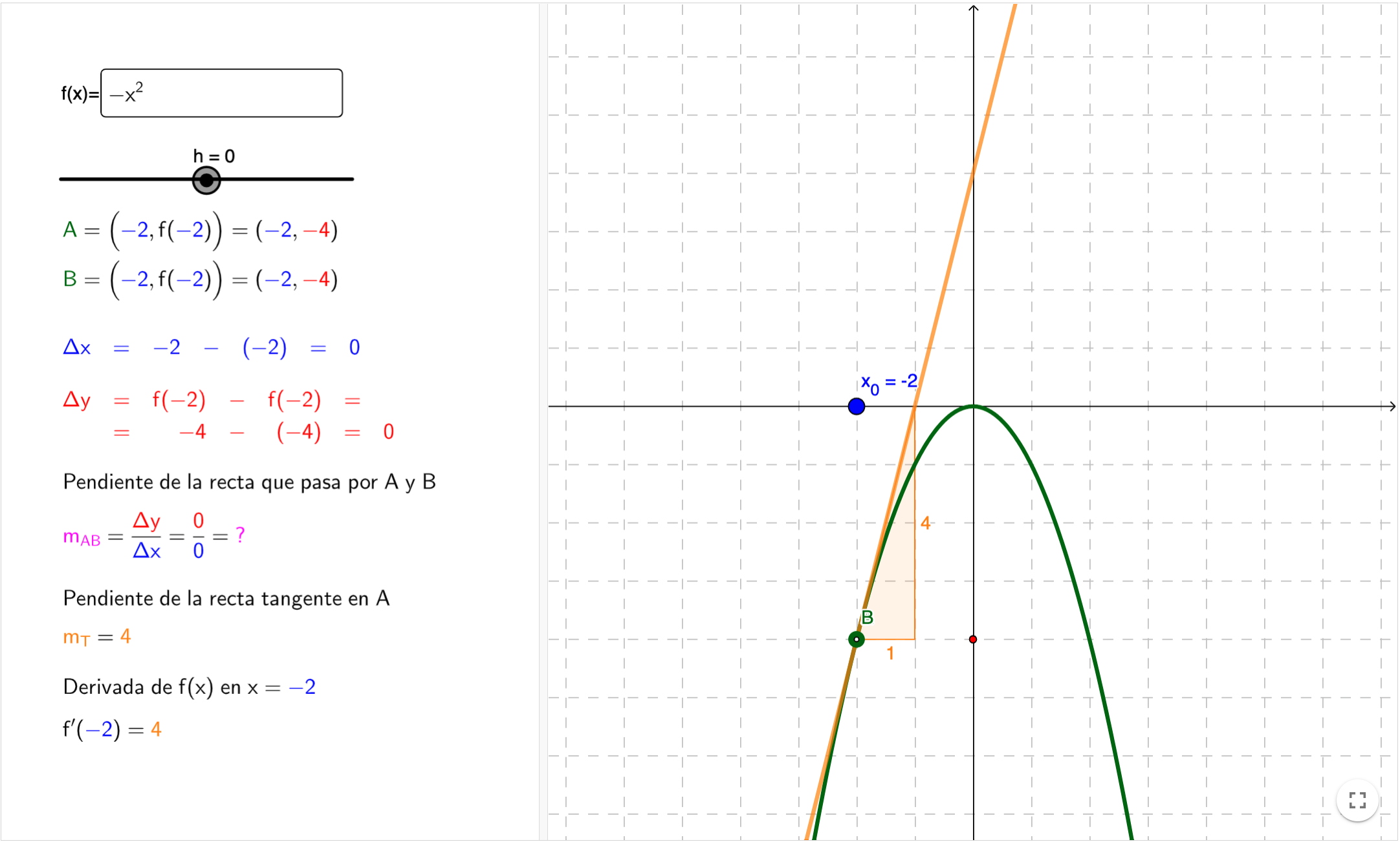
Derivada de una función en un punto
Con este recurso se puede mostrar la interpretación geométrica de la derivada de una función en un punto.
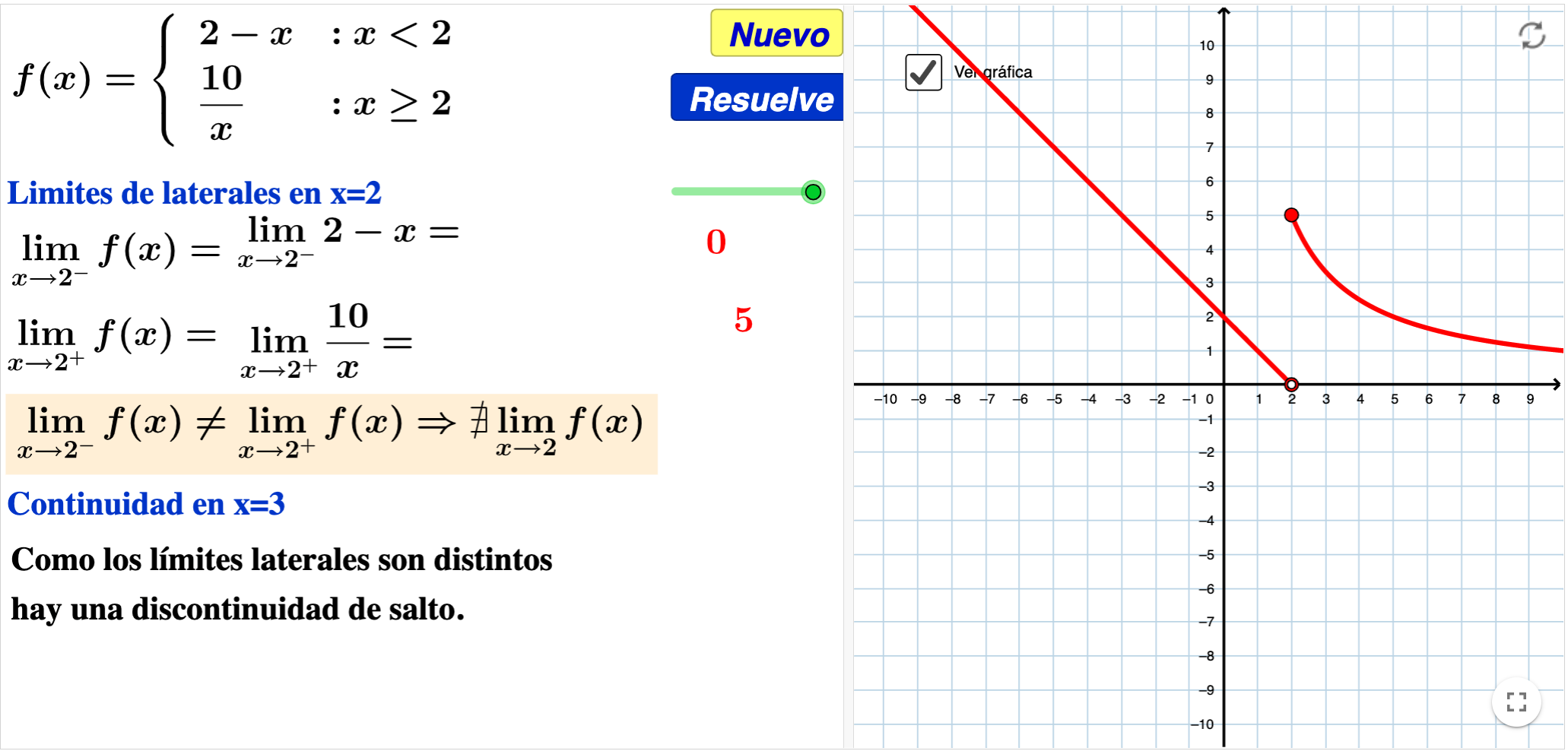
Límites laterales en una función definida a trozos
Con este recurso se puede observar el proceso para estudiar los limites laterales y la continuidad en una función definida a trozos.
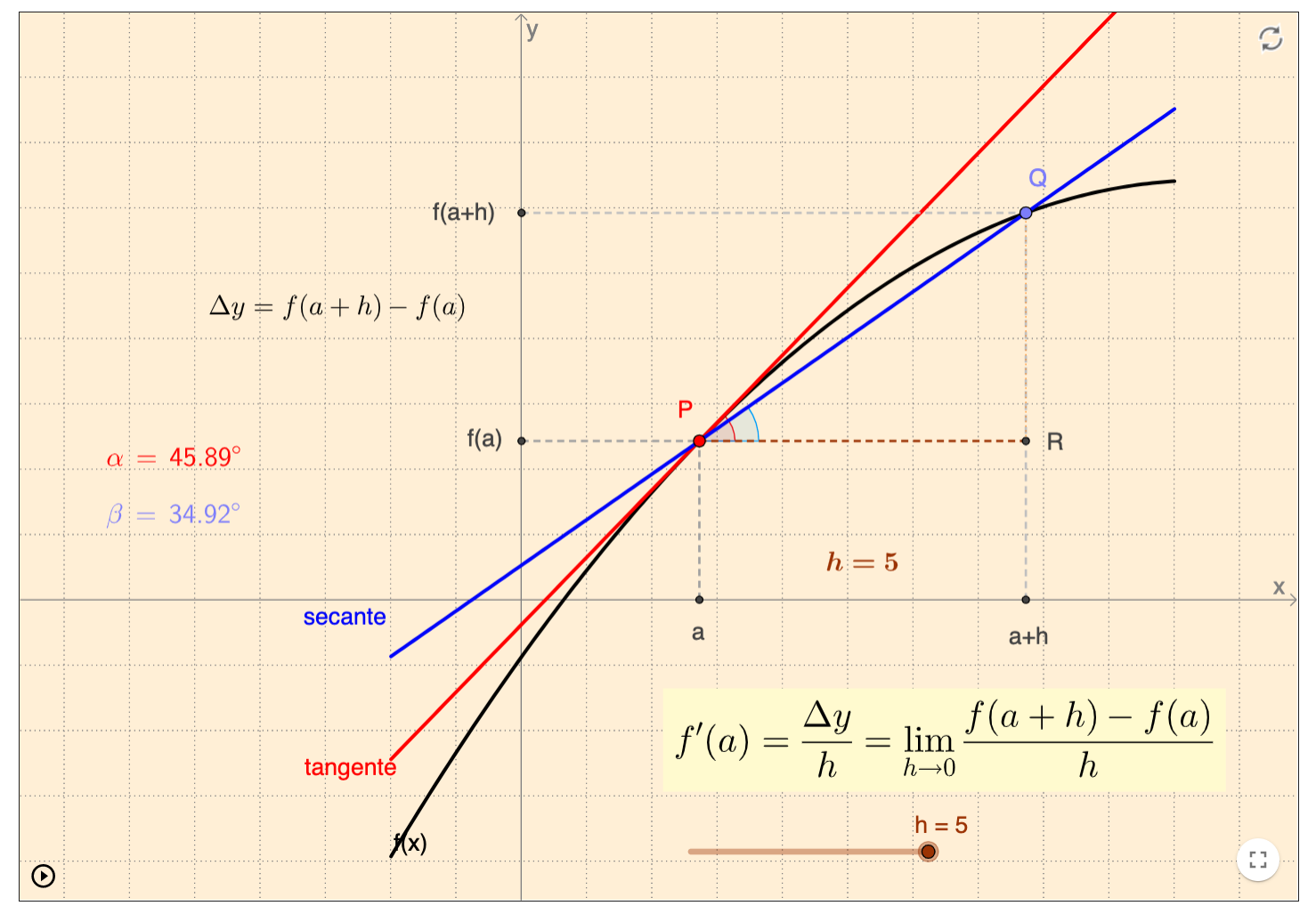
Derivada de una función en un punto
Con este recurso se puede visualizar el concepto de derivada como el límite de la tasa de variación media cuando la longitud del intervalo tiende hacia 0 relacionando dichos conceptos con las rectas tangente y secante, respectivamente.
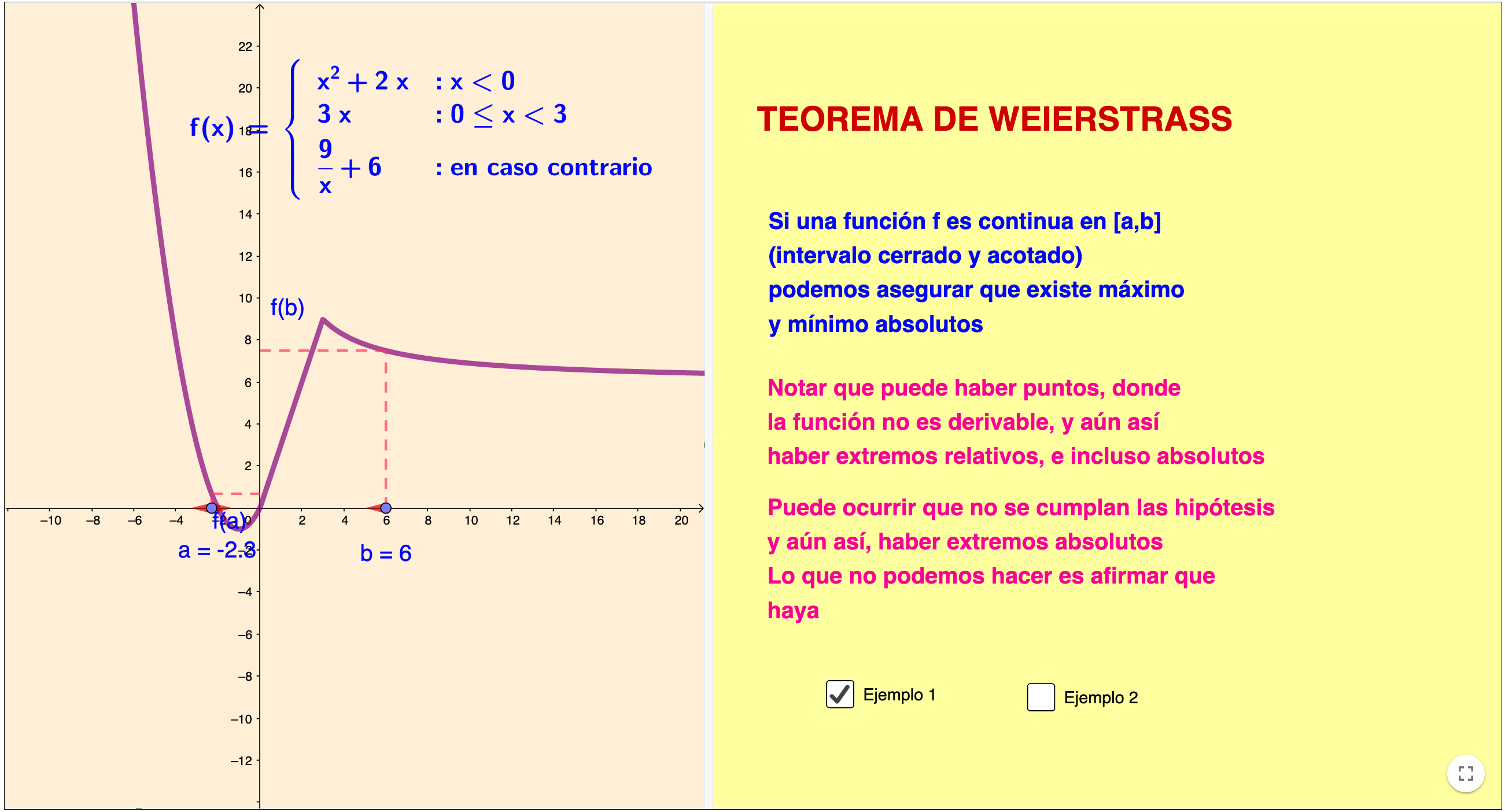
Teorema de Weierstrass
Con este recurso se pueden visualizar dos ejemplos de aplicación del teorema de Weierstrass.
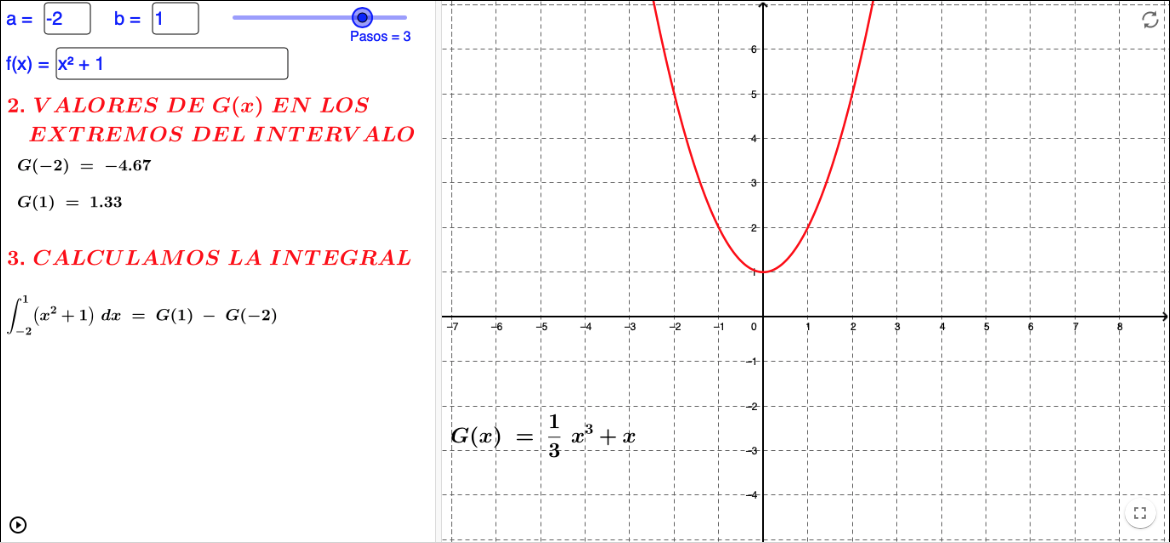
Regla de Barrow
El recurso permite introducir una función y los límites donde queramos hallar su integral definida. Permite visualizar la aplicación de la Regla de Barrow en tres pasos.
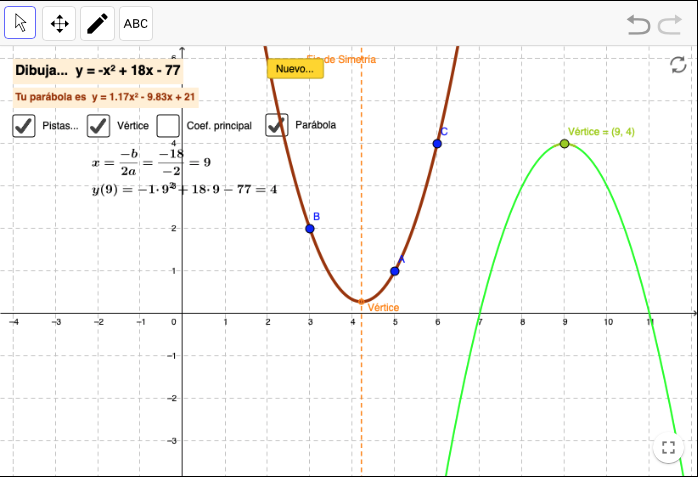
Dibuja la parábola
El recurso propone la ecuación de una parábola. En la gráfica aparece una parábola determinada por tres puntos que deben variarse hasta conseguir la parábola pedida.
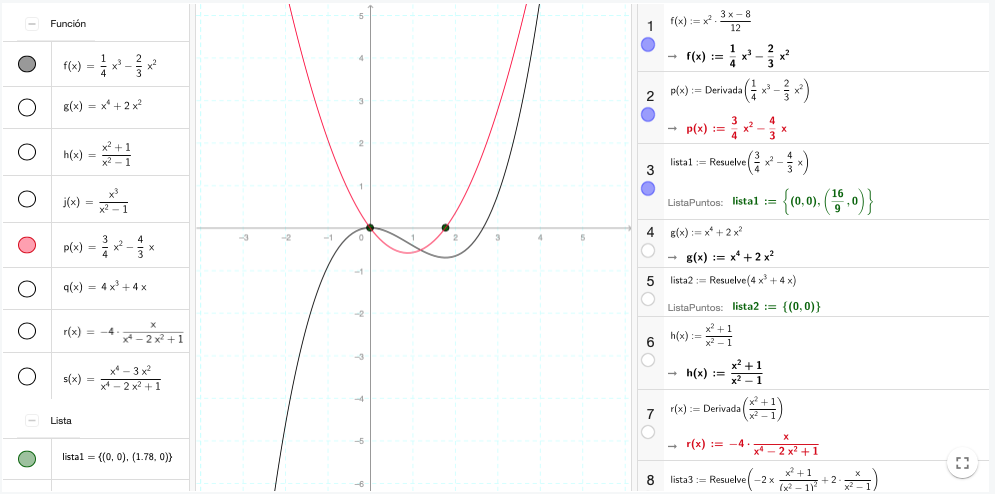
Encontrar valores donde se anule la derivada
El recurso presenta una primera lista de diferentes funciones polinómicas y racionales, que pueden visualizarse independientemente. En una segunda lista se incluyen las derivadas de las funciones anteriores y los puntos de corte de estas derivadas con el eje OX, que también pueden visualizarse a discreción.
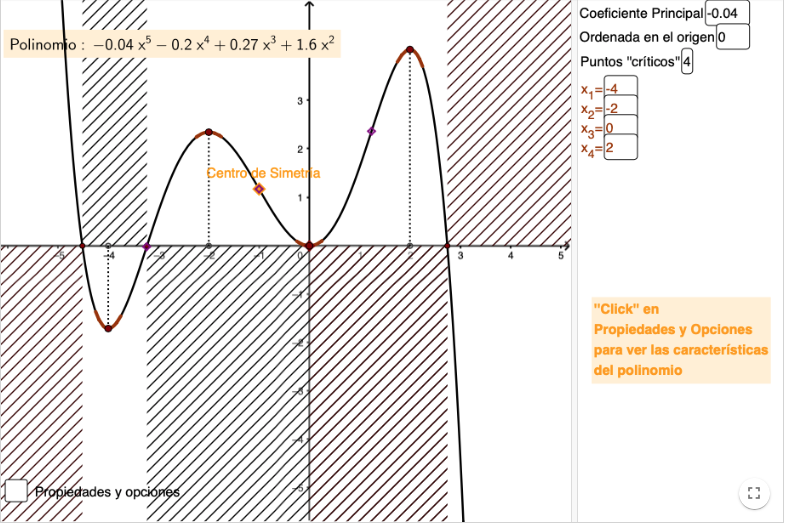
Representar polinomios conociendo sus puntos críticos
Se presenta una función polinómica de grado menor o igual que cuatro. Se puede variar el coeficiente principal, así como sus puntos críticos. Se visualizan las principales propiedades y características de la función dada.