Buscador global
Mostrando del 1 al 10 de 12 resultados para: Nearpod: mucho más que una aplicación interactiva filtrando por: Propuesta didácticaLímite
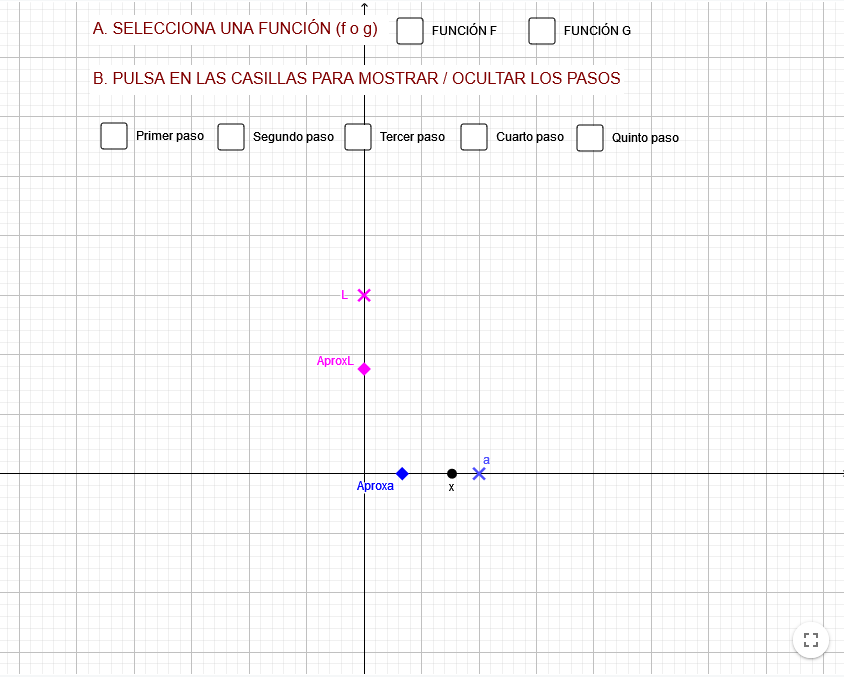
Límite de una función en un punto
El recurso utiliza un applet con dos funciones, una de ellas con una discontinuidad evitable y otra con una discontinuidad con salto finito, y varias casillas que se van marcando para guiar la introducción al concepto de límite finito en un punto, desde una aproximación intuitiva hasta la formalización. En el propio applet aparecen las instrucciones según se marcan las casillas. Además, se proponen una serie de cuestiones, basadas en la experimentación con el applet, que guían la secuencia.
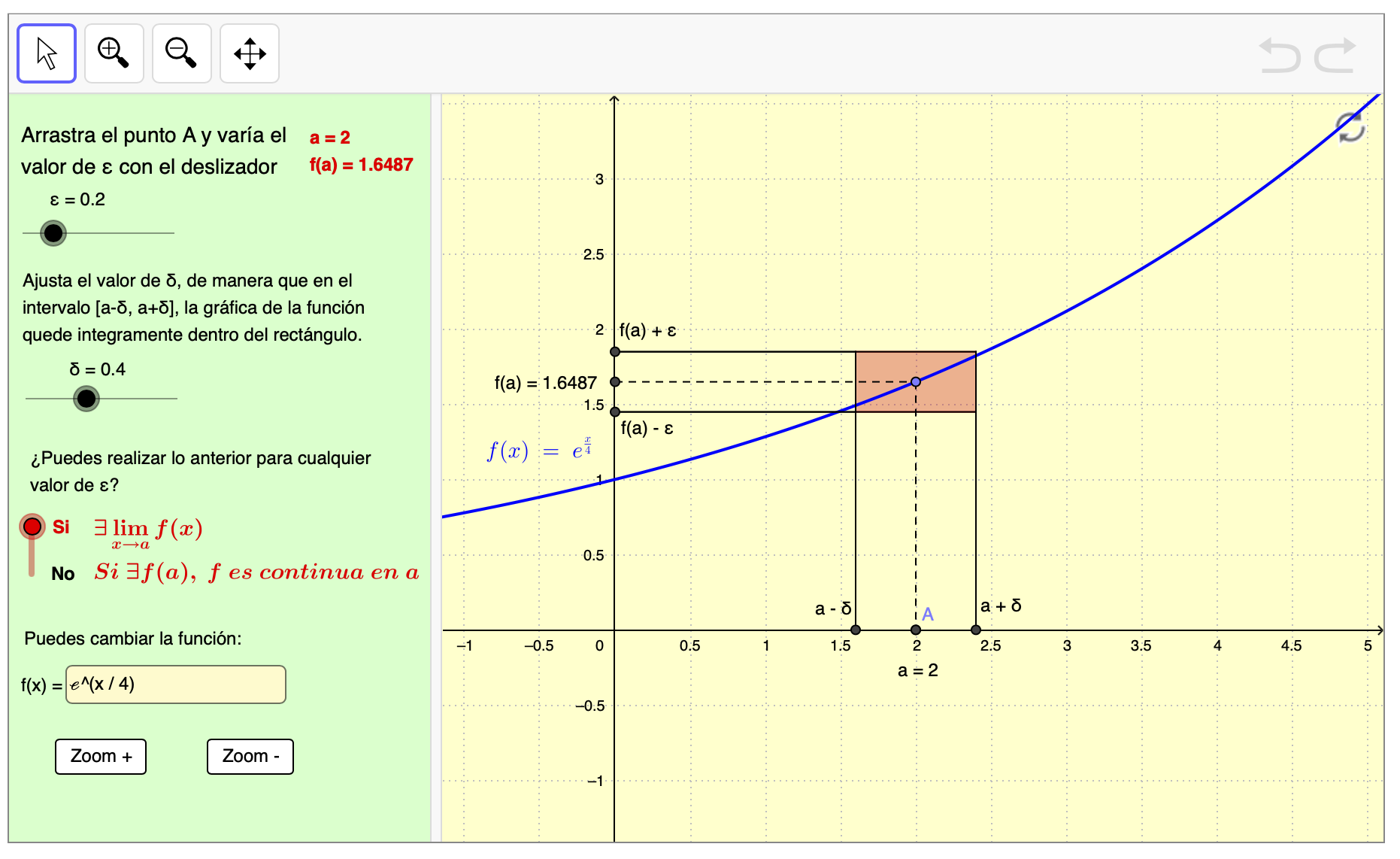
Límite y continuidad de una función en un punto
Applet que permite trabajar gráfica y numéricamente sobre la definición formal de límite finito de una función en un punto.
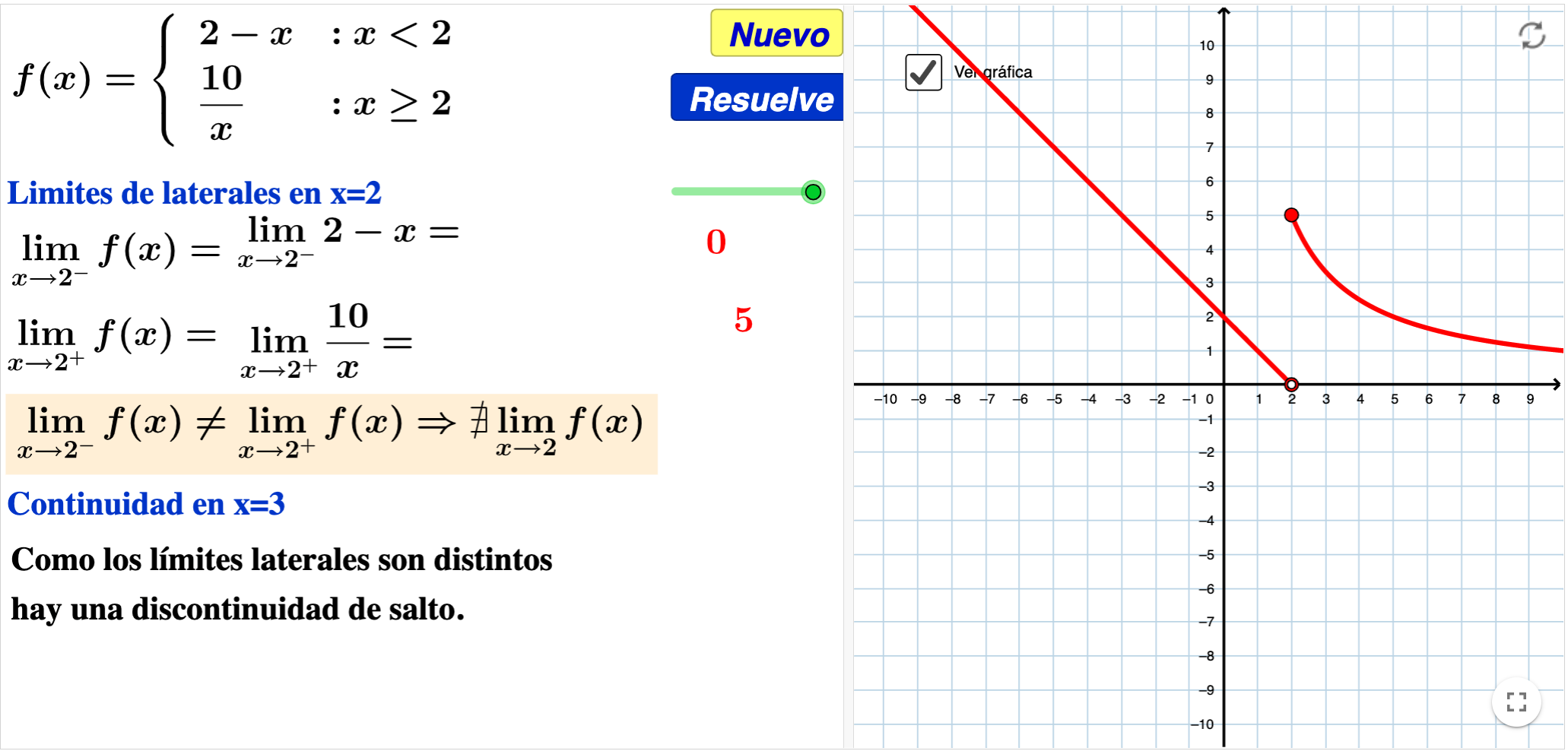
Límites laterales en una función definida a trozos
Con este recurso se puede observar el proceso para estudiar los limites laterales y la continuidad en una función definida a trozos.
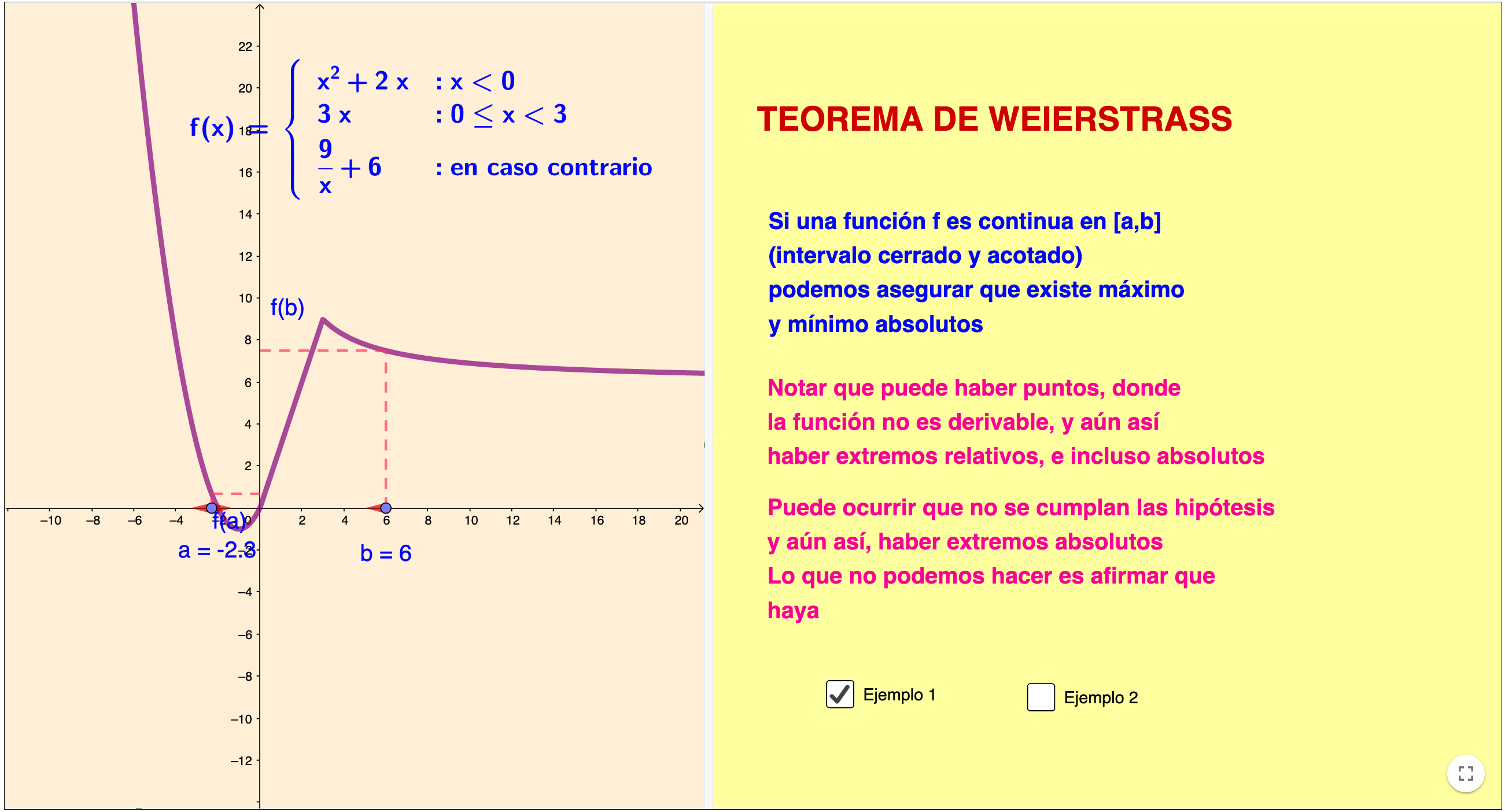
Teorema de Weierstrass
Con este recurso se pueden visualizar dos ejemplos de aplicación del teorema de Weierstrass.
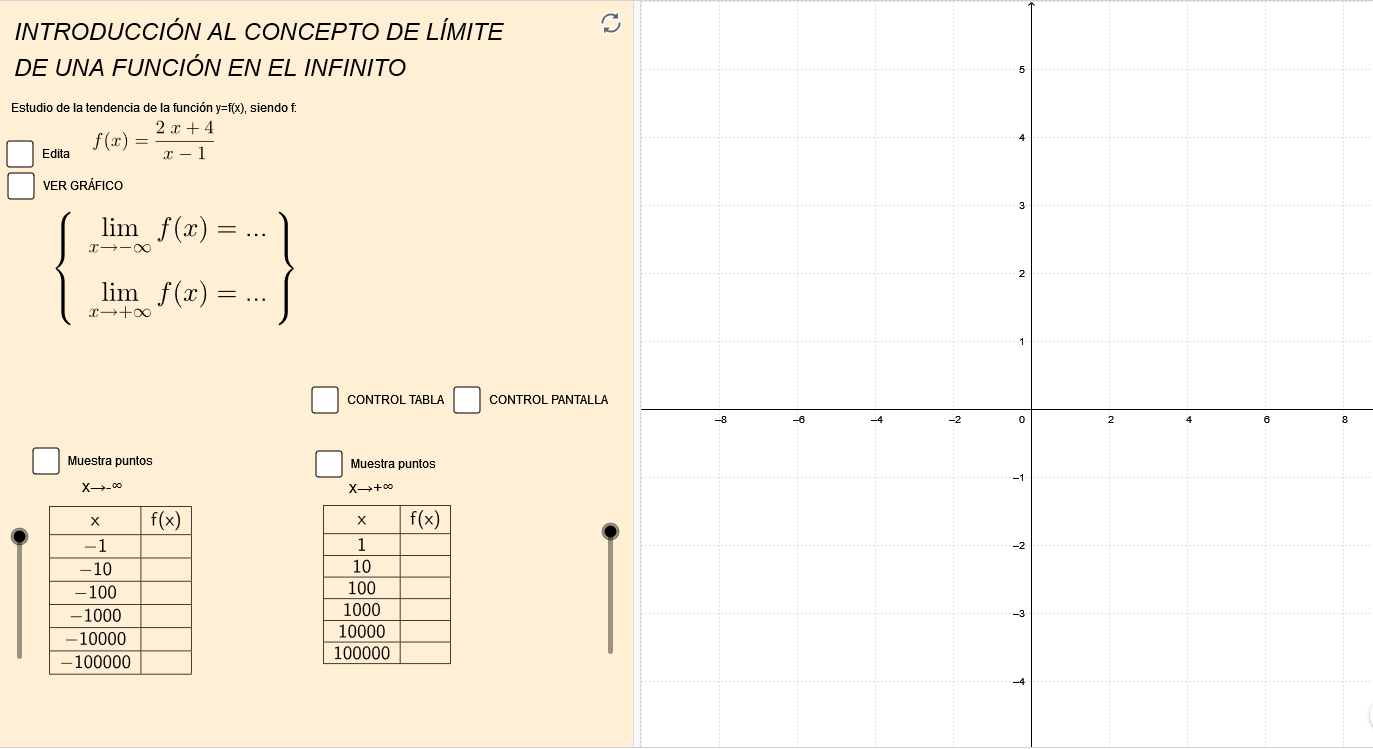
Límite en el infinito
Introduce el concepto de límite cuando x tiende a más o menos infinito de forma gráfica y numérica, pudiendo modificar la función.
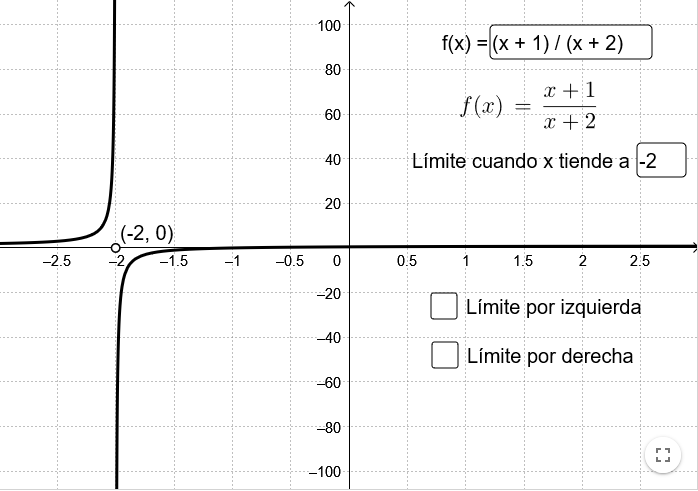
Límites laterales
Applet en el que se introduce la expresión de una función y un valor para x y muestra la aproximación por la derecha y por la izquierda a dicho valor de x.
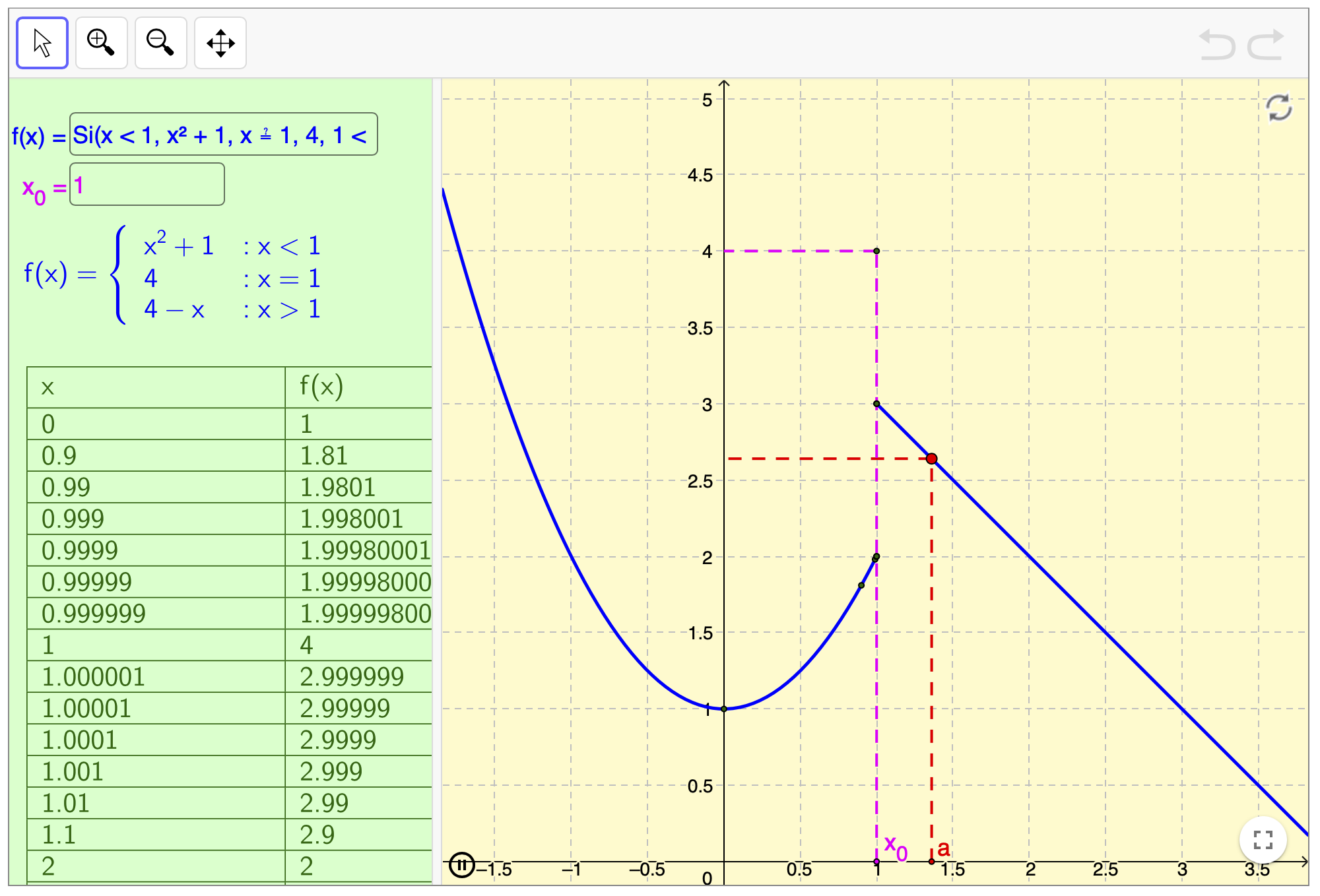
Aproximación numérica al límite en un punto
Applet explicativo sobre límite de una función en un punto.
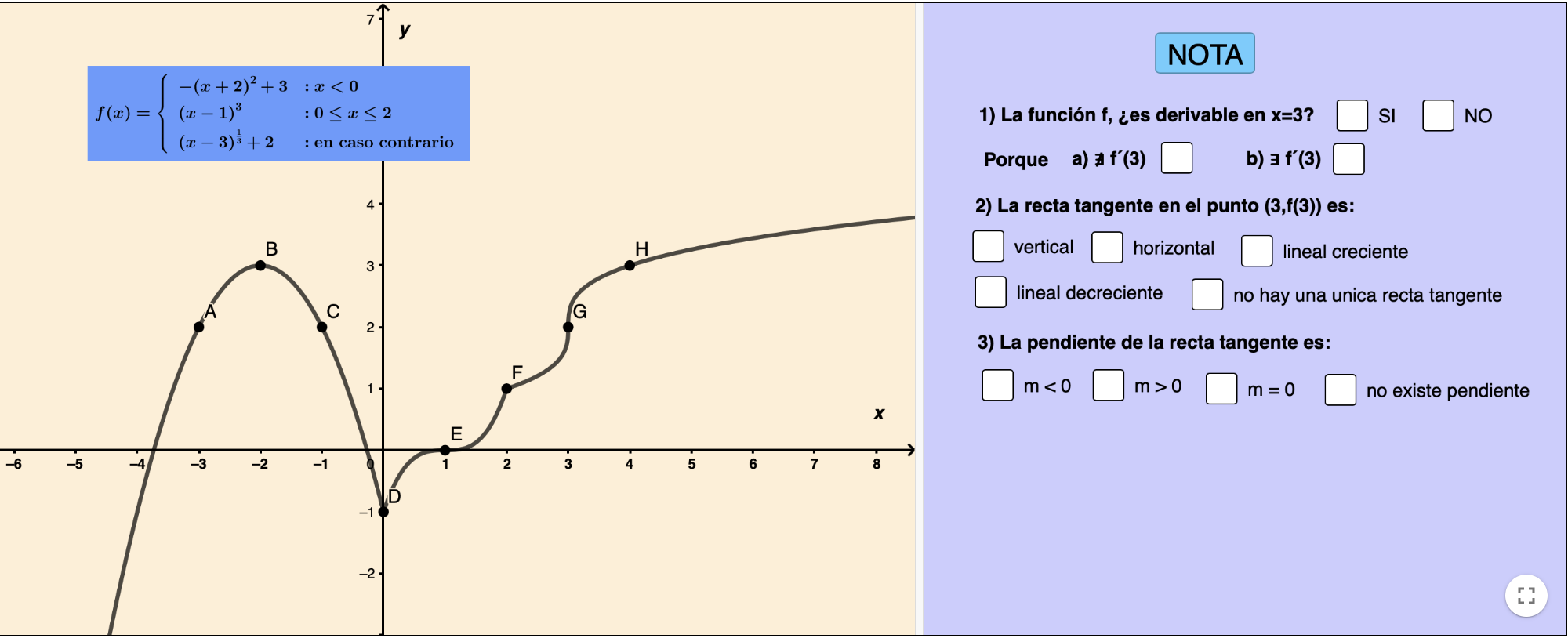
Derivabilidad
Se muestra la gráfica de una función preguntando su derivabilidad en diferentes puntos.
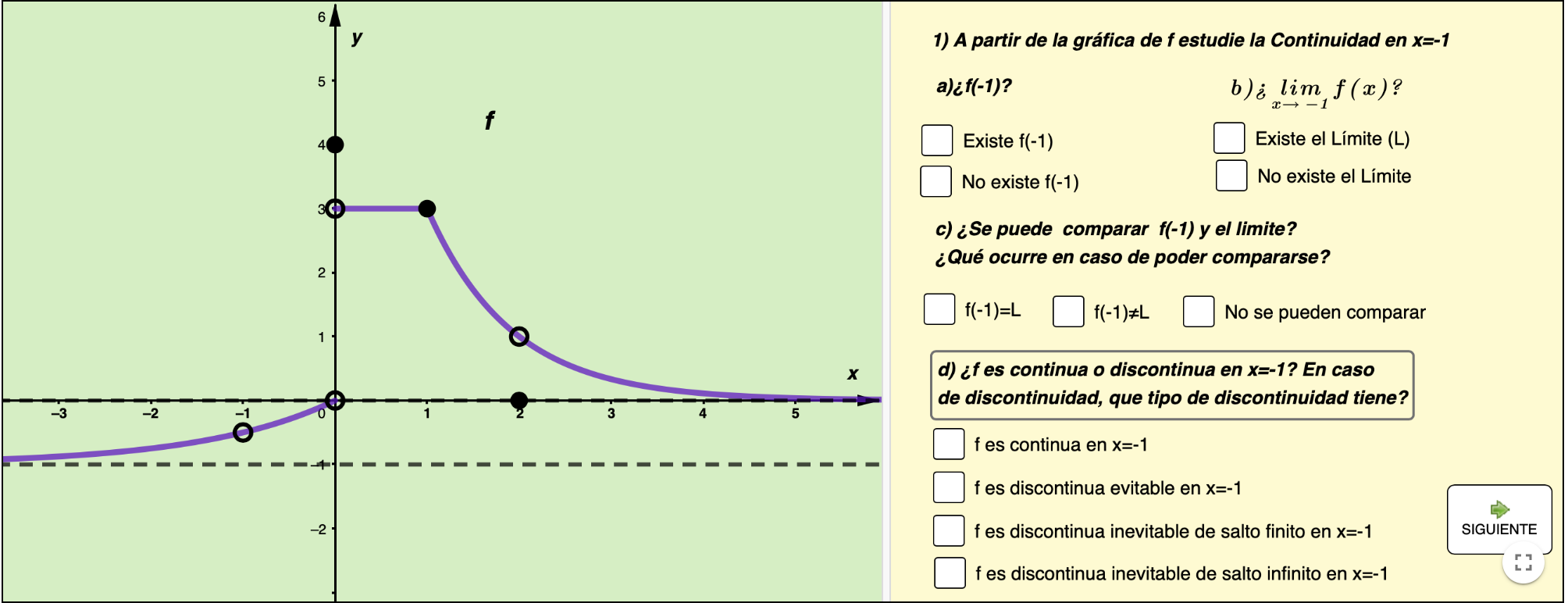
Límite. Continuidad. Discontinuidad.
El recurso muestra aleatoriamente una función de entre tres posibles, preguntando los aspectos fundamentales de la continuidad.
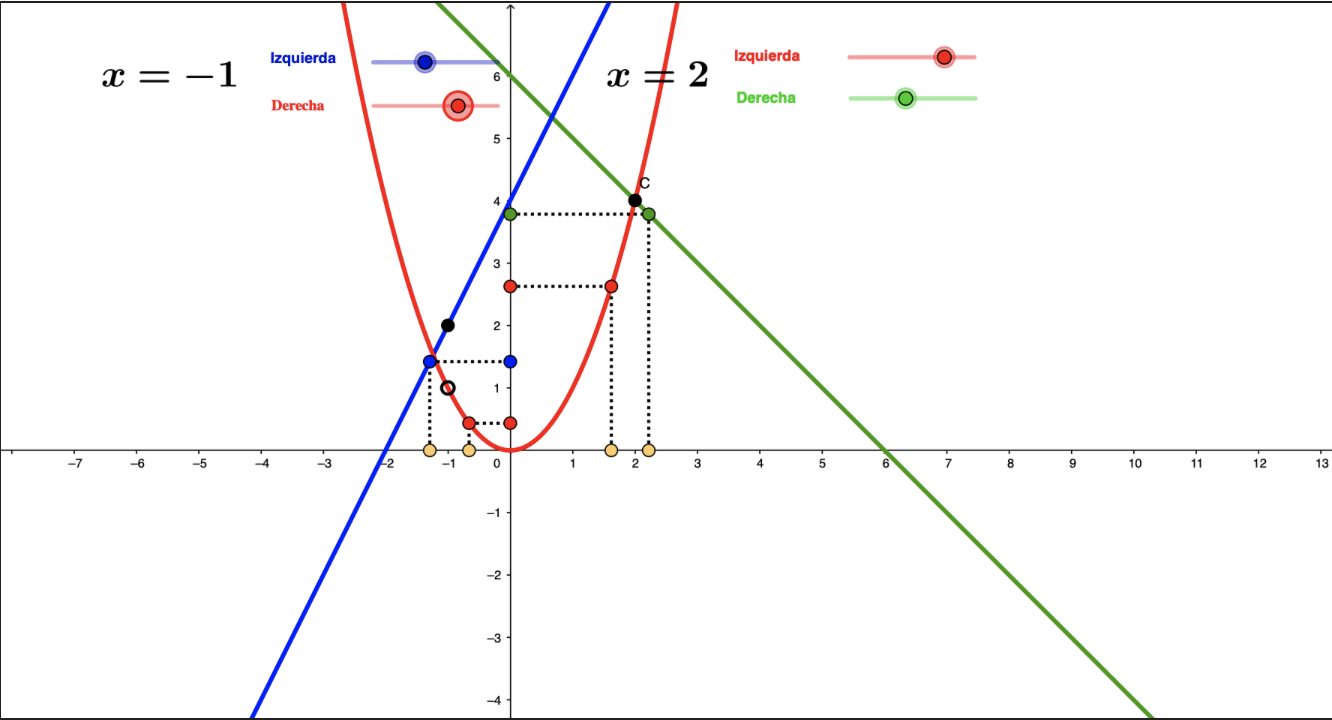
Límites laterales, límite, continuidad
El recurso muestra una función definida a trozos, varios deslizadores permiten comprobar si los límites laterales coinciden, y por tanto si existe continuidad.