Buscador global
Mostrando del 21 al 30 de 152 resultados para: Nearpod: mucho más que una aplicación interactiva filtrando por: Función
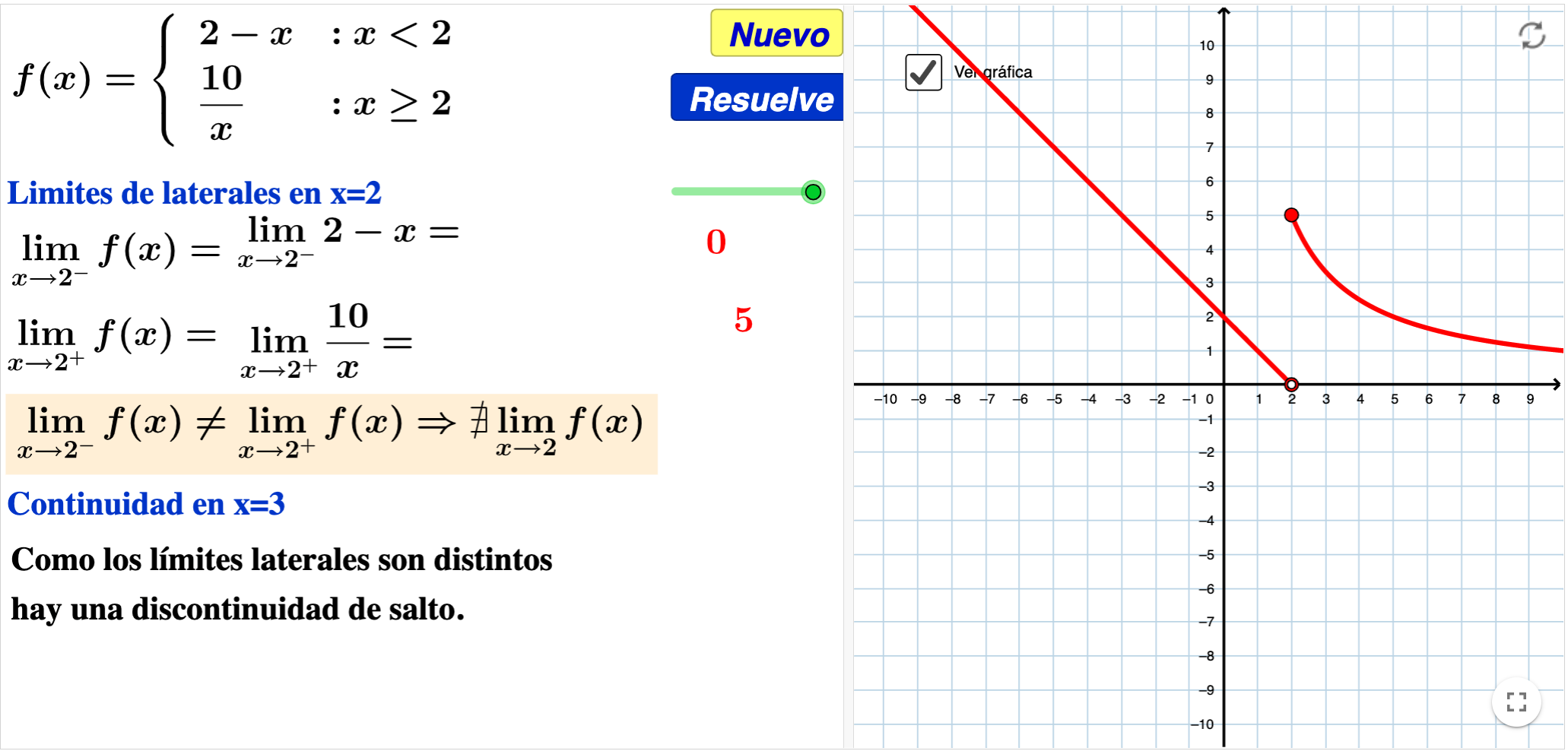
Límites laterales en una función definida a trozos
Con este recurso se puede observar el proceso para estudiar los limites laterales y la continuidad en una función definida a trozos.
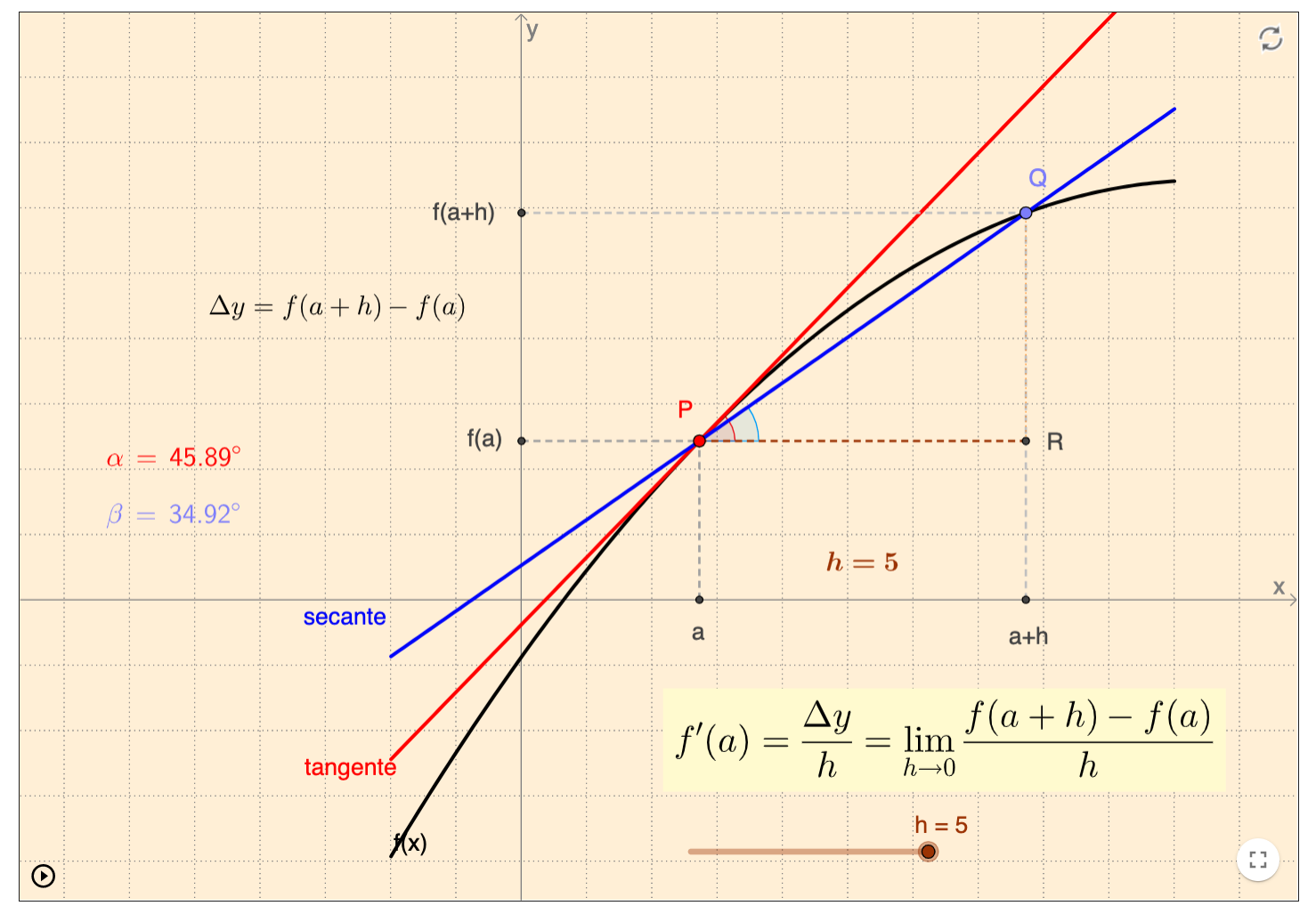
Derivada de una función en un punto
Con este recurso se puede visualizar el concepto de derivada como el límite de la tasa de variación media cuando la longitud del intervalo tiende hacia 0 relacionando dichos conceptos con las rectas tangente y secante, respectivamente.
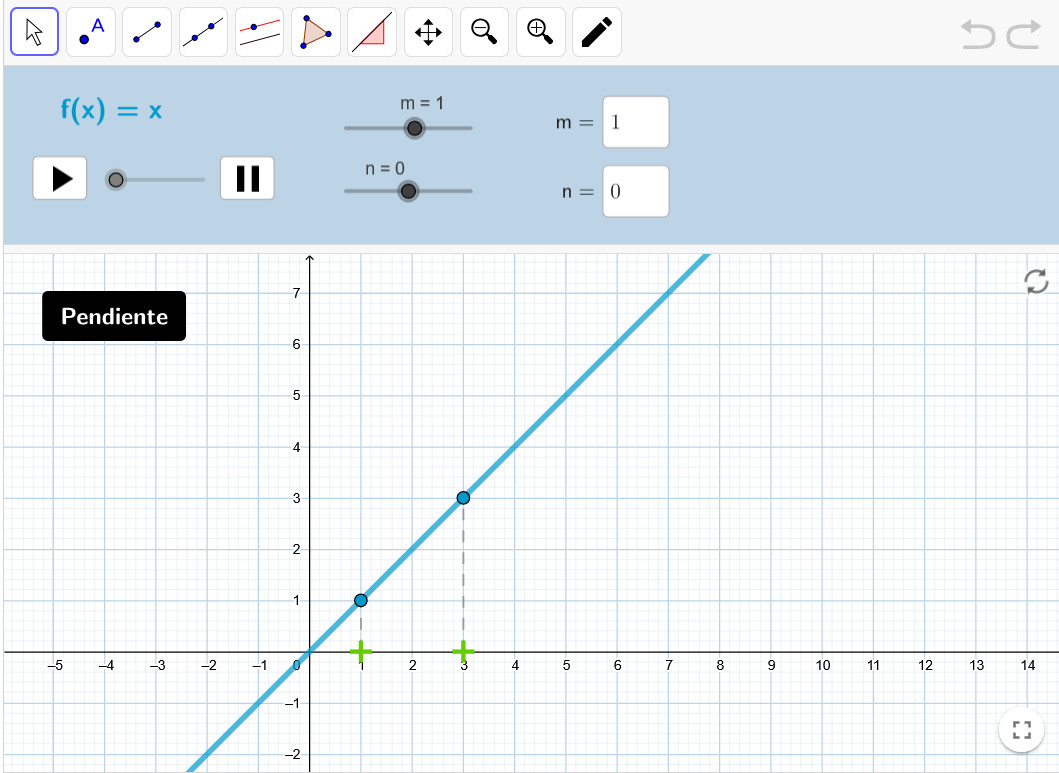
Pendiente y ordenada en el origen de una función lineal
Permite observar la representación gráfica de una función lineal a partir de unos valores dados de la pendiente y la ordenada en el origen.
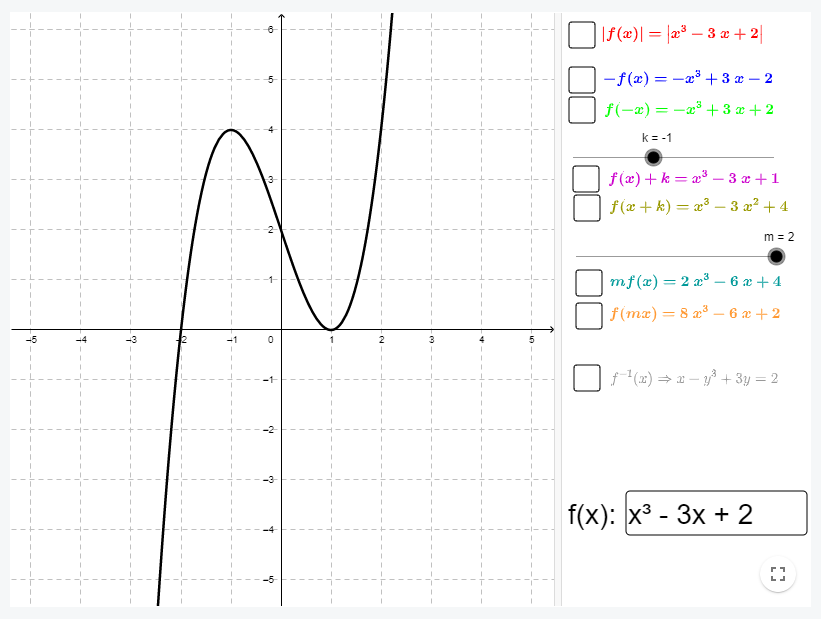
Transformaciones de funciones
Applet de Geogebra que presenta el efecto de las diferentes transformaciones en la expresión algebraica de cualquier función en la gráfica correspondiente.
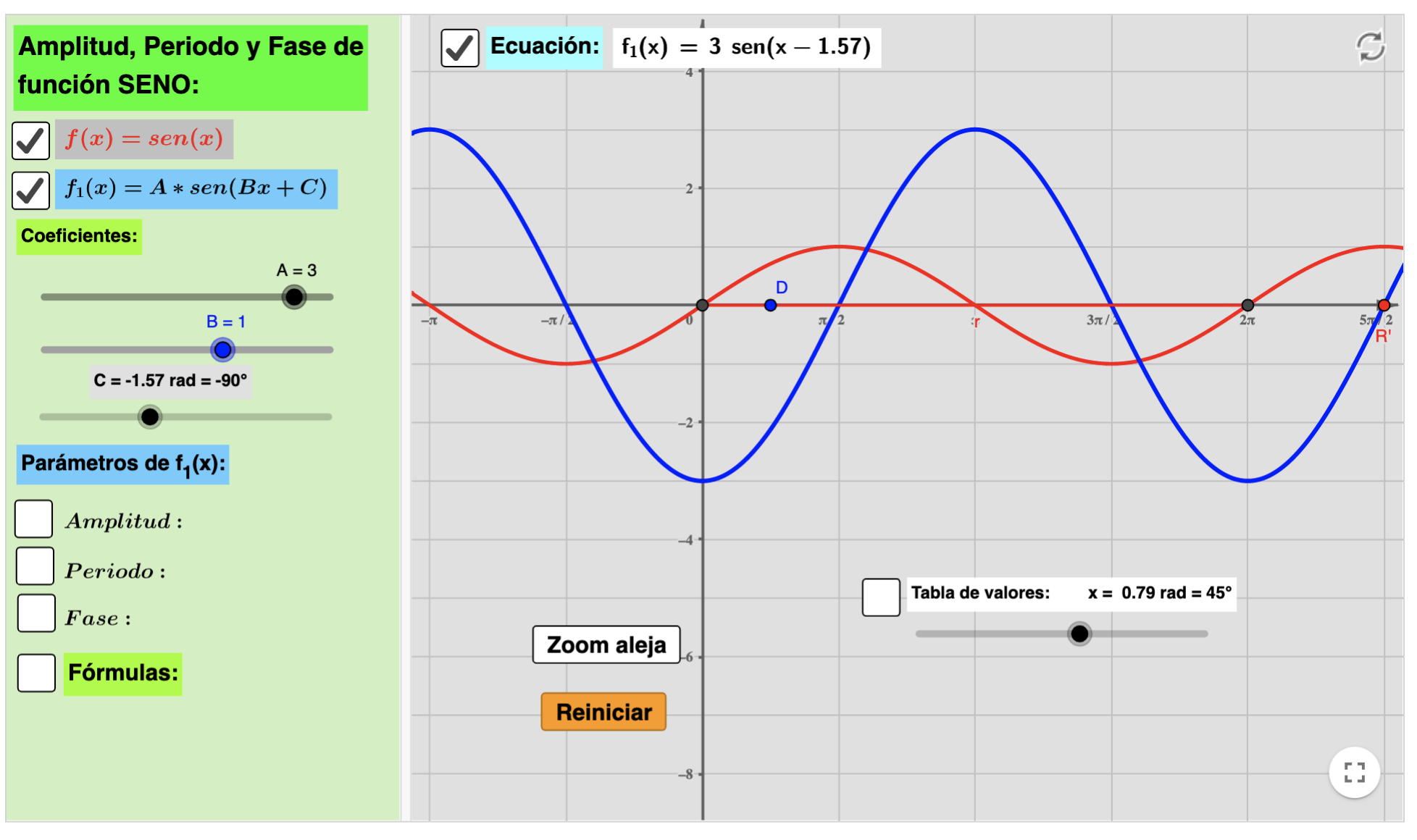
Amplitud, periodo y fase de funciones sinusoidales
Estudio de las funciones sinusoidales y su aplicación como ecuación de onda.
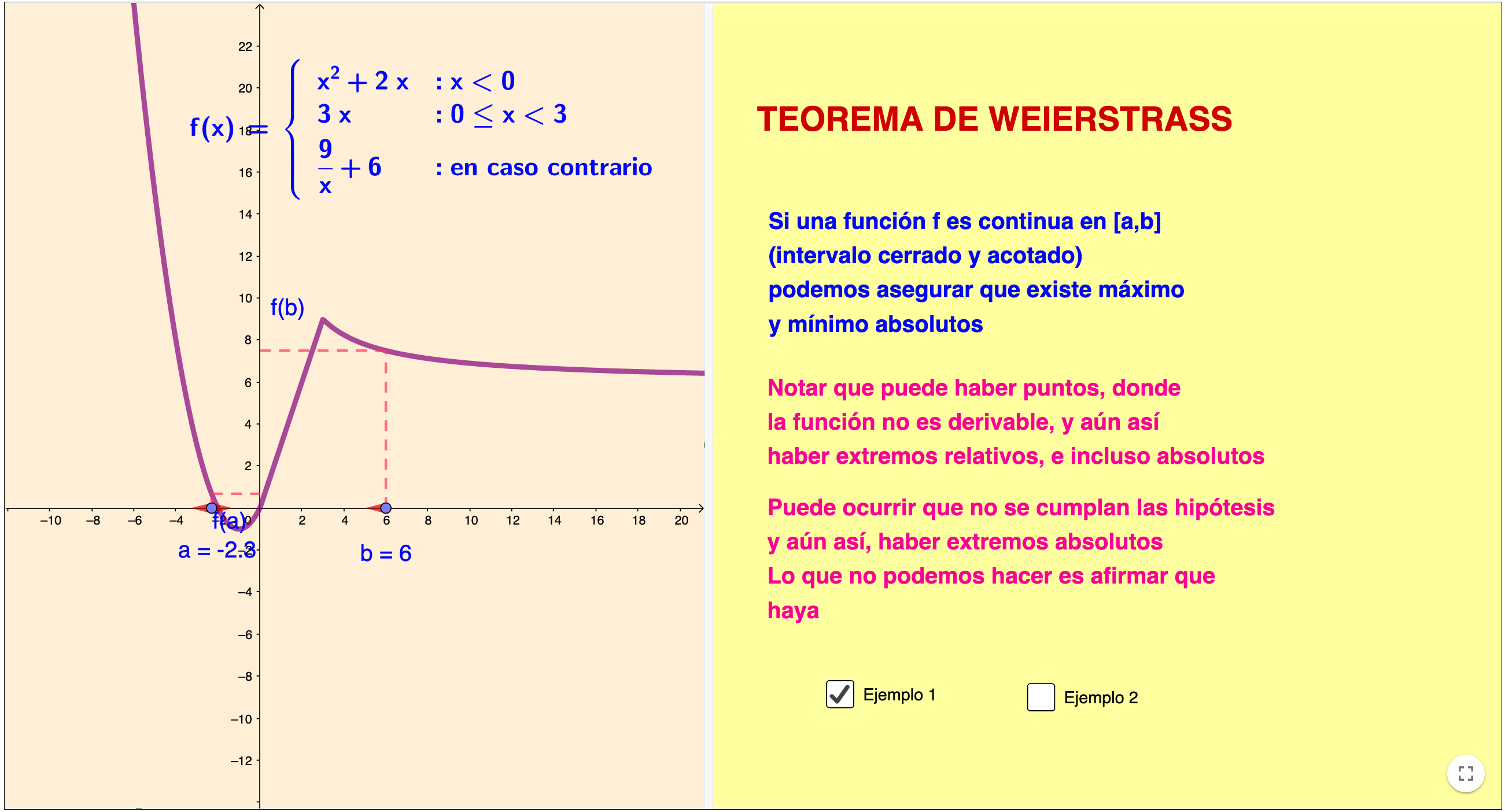
Teorema de Weierstrass
Con este recurso se pueden visualizar dos ejemplos de aplicación del teorema de Weierstrass.
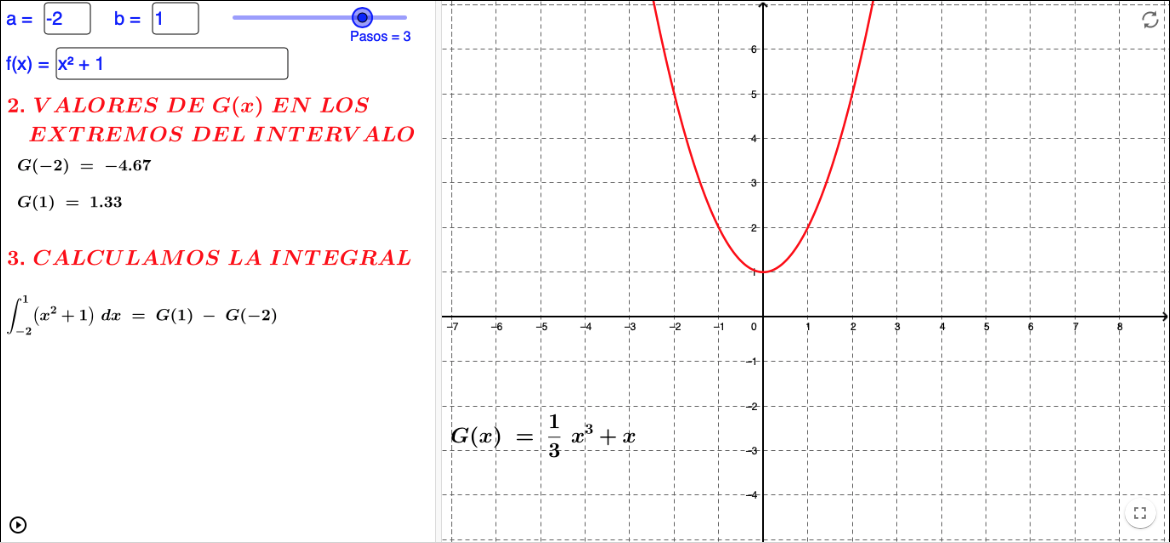
Regla de Barrow
El recurso permite introducir una función y los límites donde queramos hallar su integral definida. Permite visualizar la aplicación de la Regla de Barrow en tres pasos.
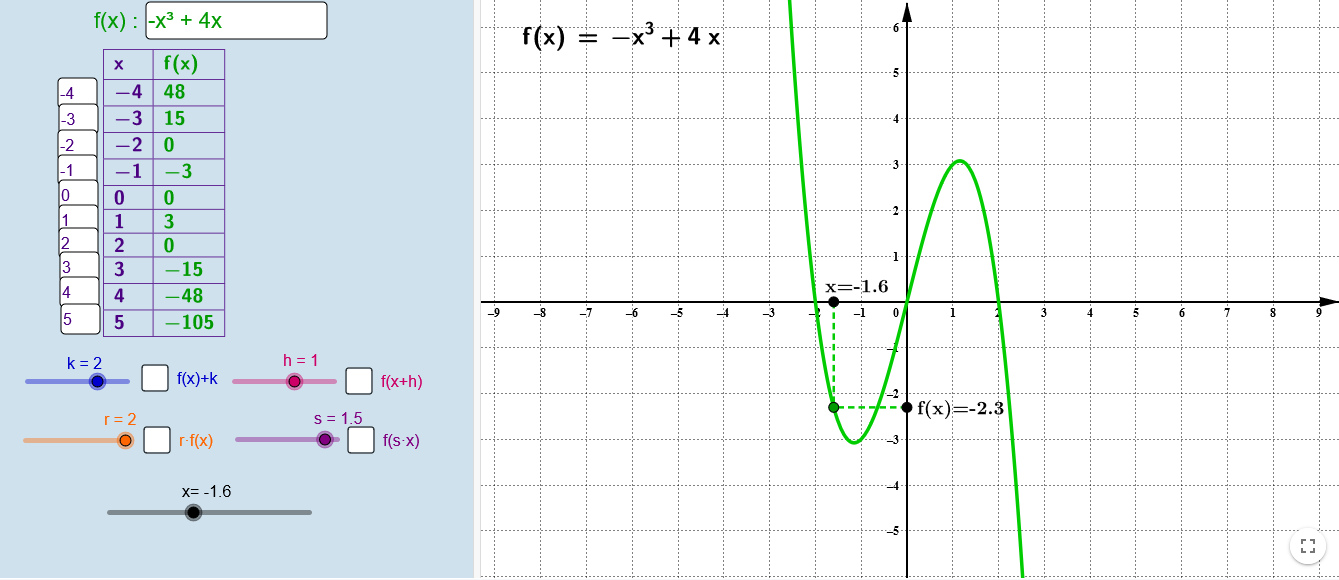
Transformaciones funciones
El applet muestra la gráfica de una función (que se puede modificar) y su tabla de valores, y permite visualizar los cuatro tipo de transformaciones más comunes observando el efecto que produce sobre la gráfica original (y también su tabla de valores).
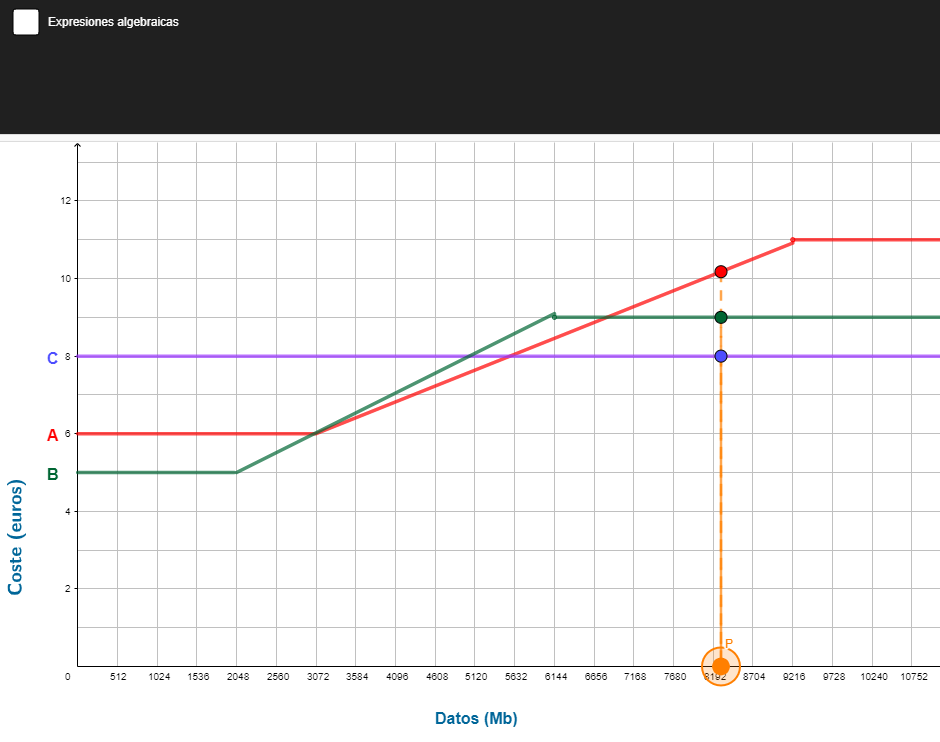
Tarifas de datos
En este applet se nos muestra la gráfica de tres compañías de teléfono. El alumno tiene que identificar qué tarifa es la más adecuada en función de los datos que consuma al mes.
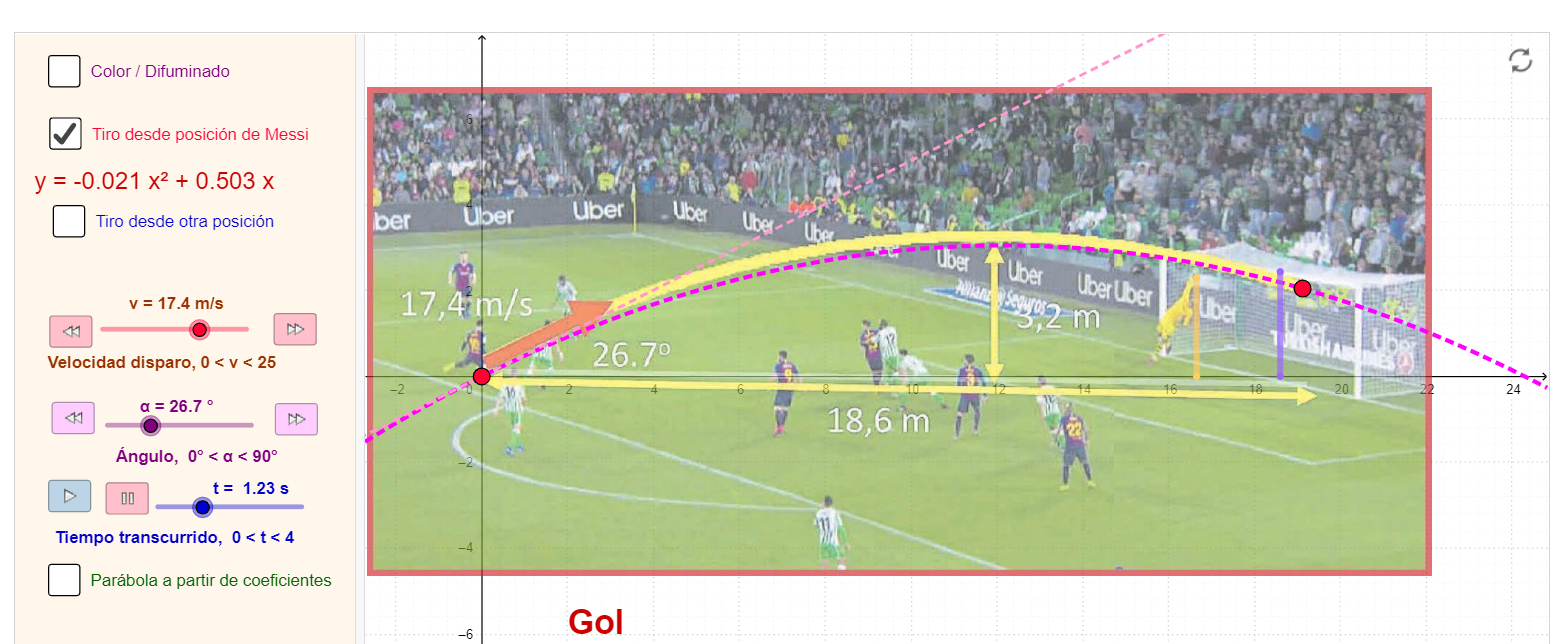
Parábolas y fútbol
Analizando un disparo a portería en un partido de fútbol, se estudia la trayectoria parabólica. Además se propone profundizar más hallando las ecuaciones de movimiento.