Buscador global
Mostrando del 1 al 10 de 32 resultados para: Nearpod: mucho más que una aplicación interactiva filtrando por: ESO5º E.P.
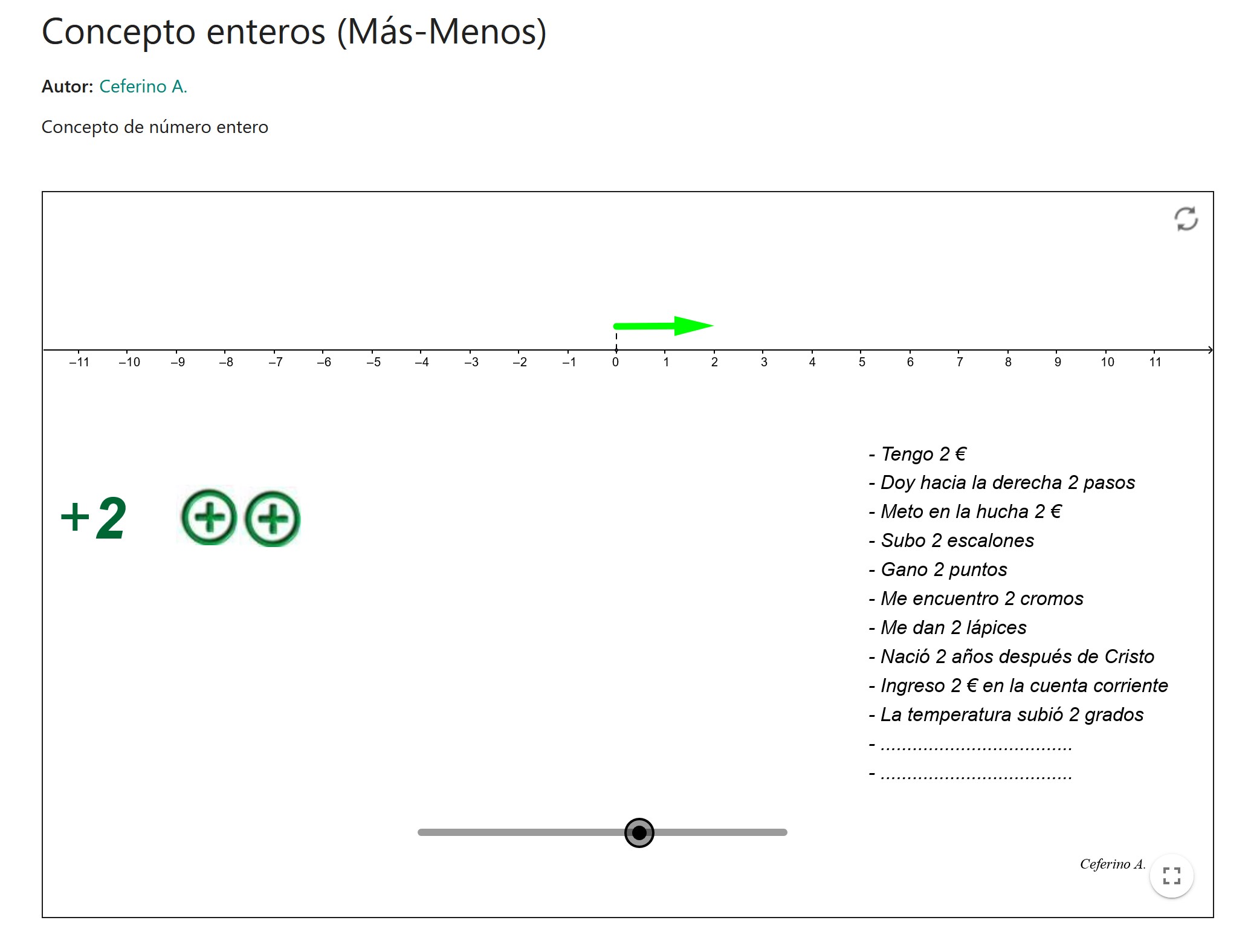
Concepto enteros (Más-Menos)
El applet puede usarse durante la introducción al concepto de número entero (positivo y negativo). Aparecen los números del -10 al 10, su representación con fichas positivas y negativas, en la recta numérica y un listado de frases de aplicación del número en situaciones reales.
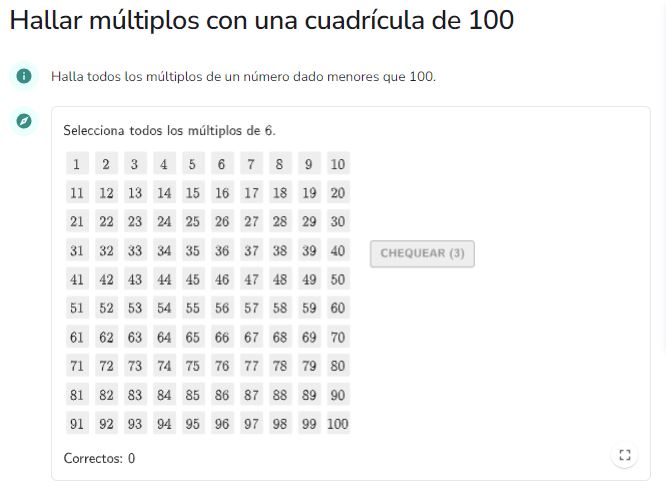
Hallar múltiplos con una cuadrícula de 100
El applet presenta los 100 primeros números naturales en una cuadrícula de 10x10, y donde se debe marcar los números de dicha cuadrícula que son múltiplos de uno dado. Además el applet ofrece corrección sobre la selección realizada. De esta forma se pueden estudiar regularidades y patrones de dichos múltiplos.
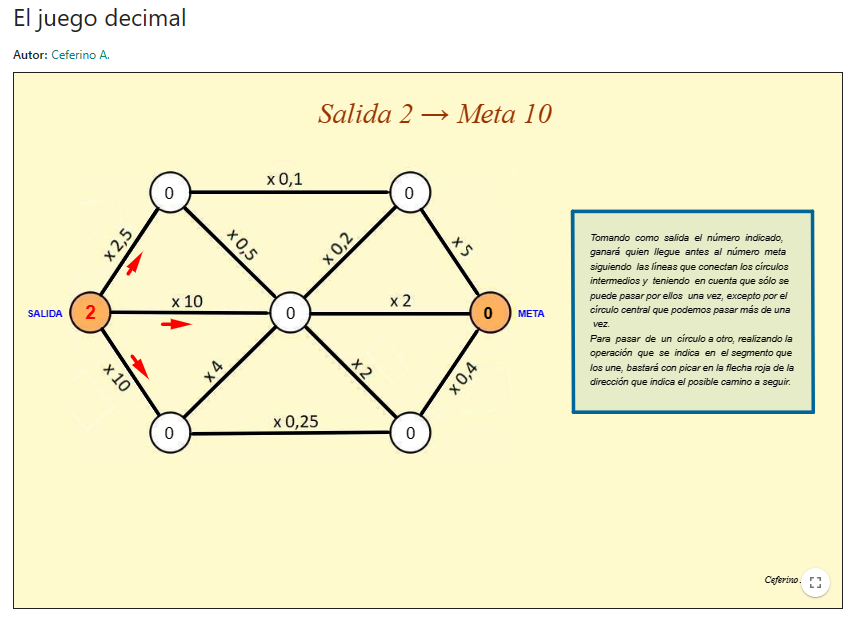
El juego decimal
El applet presenta un reto a modo de juego sobre cómo ir de una casilla de salida a otra de meta con la opción de poder elegir diferentes caminos donde para pasar de una casilla a otra es necesario realizar multiplicación de números racionales como 2,5; 0,2; 5; 10; 2; 0,4; 0,5; 0,1 o 0,25. El reto presenta además otras condiciones, como que el número de meta debe de ser uno determinado y hay una casilla por la que se puede pasar más de una vez. Además una vez que se seleccione el camino, el propio applet realiza la operación.
Creación de diagramas de puntos y tablas
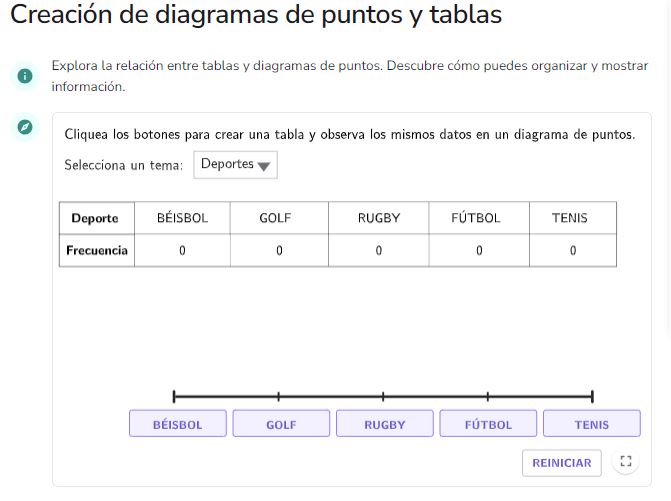
El applet presenta una tabla de datos (que tiene sus valores a 0) que se acompaña con un texto explicativo, para construir a partir de un contexto (se pueden elegir hasta tres: Deportes, Asignatura y Música) un diagrama de puntos que a su vez modifica los datos recogidos en la tabla. El gráfico se presenta con unos botones en su parte inferior donde cada vez que se pulsa en él se realiza una marca, que se debe hacer tantas veces como la persona usuaria quiera, viendo como esta marca afecta al contenido de datos de la tabla. Cuando se está modificando el diagrama de puntos, el dato correspondiente en la tabla se pondrá de color rosado, y cuando ya no se pueda poner más marcas (es limitado) el botón deja de poder usarse (se pone gris). El applet permite experimentar la relación que hay entre las marcas de un diagrama de puntos y los datos de una tabla.
Biop
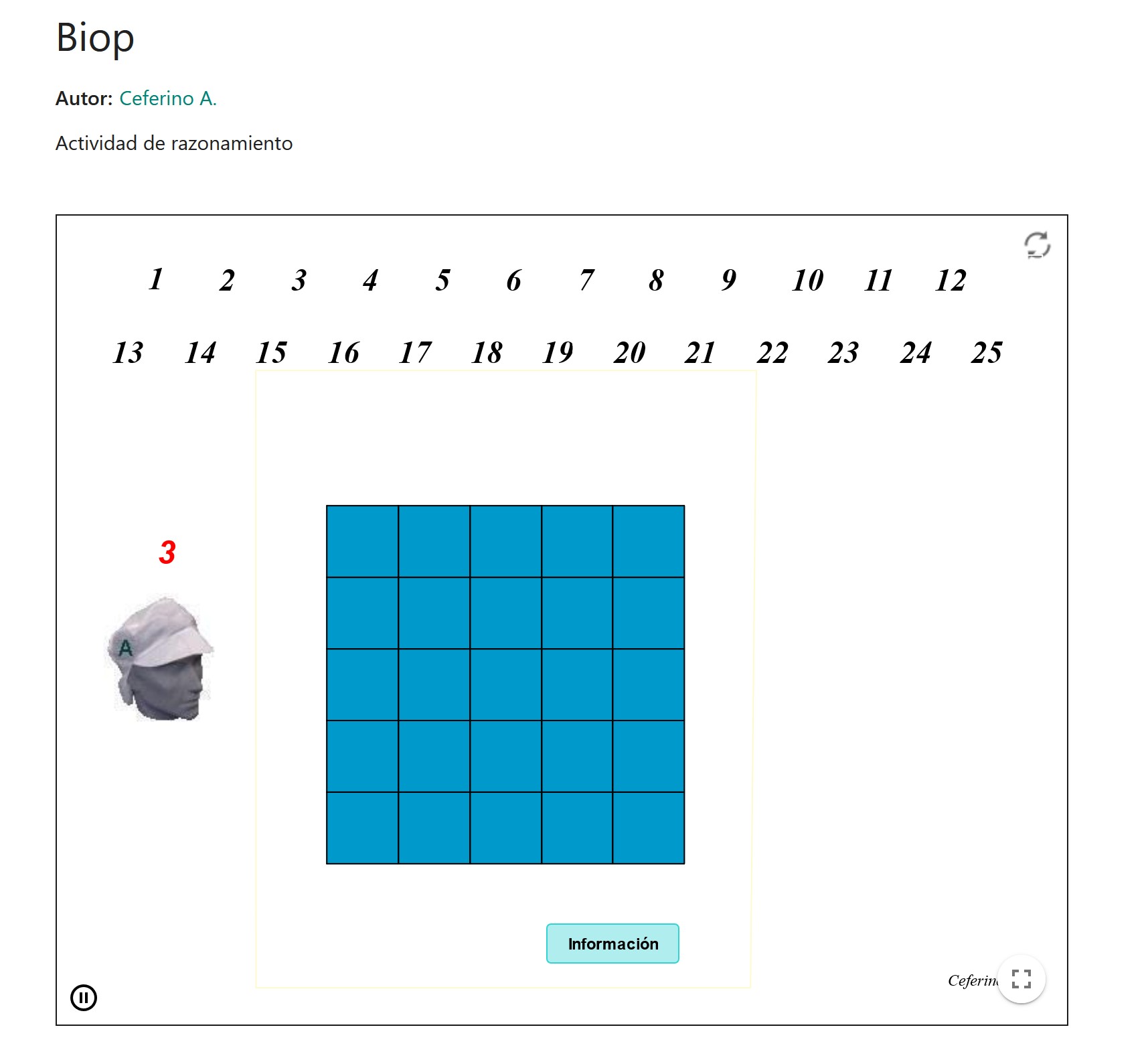
El applet presenta un juego por parejas en el que hay que rellenar, por turnos, una cuadrícula de tamaño 5x5 con los 25 primeros números de tal forma que no puede colocarse un número en una casilla que genere dos números consecutivos en cuadrículas adyacentes. Pierde quien incumpla esta norma.
¿Cuántos cubitos hay? (x4)
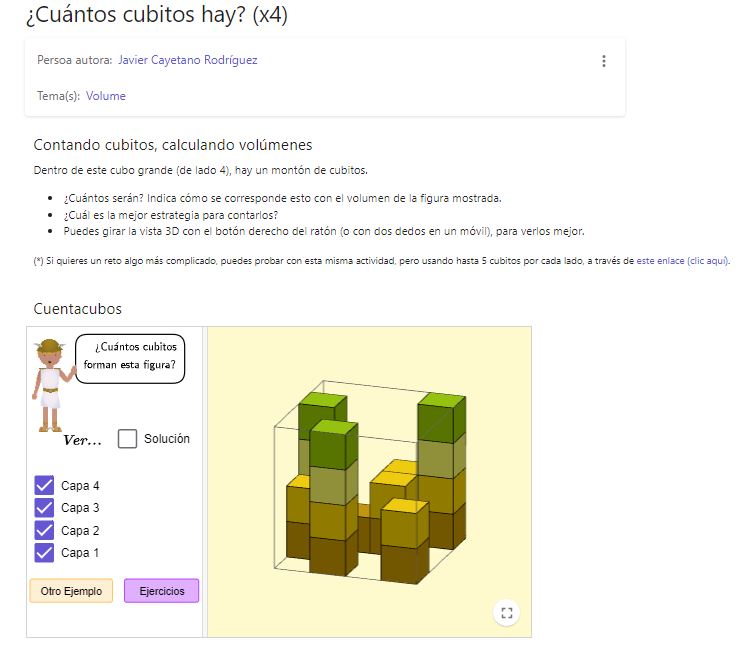
El recurso presenta una actividad donde se recoge un primer applet que presenta una figura formada por cubitos y hay que hallar el volumen que ocupa. Además permite para verificar el recuento de cubitos ver la figura por capas, facilitando así el conteo. También presenta otro applet para trabajar el volumen de octaedros. Se presenta un texto que va guiando la manipulación del recurso.
Puzle de colores
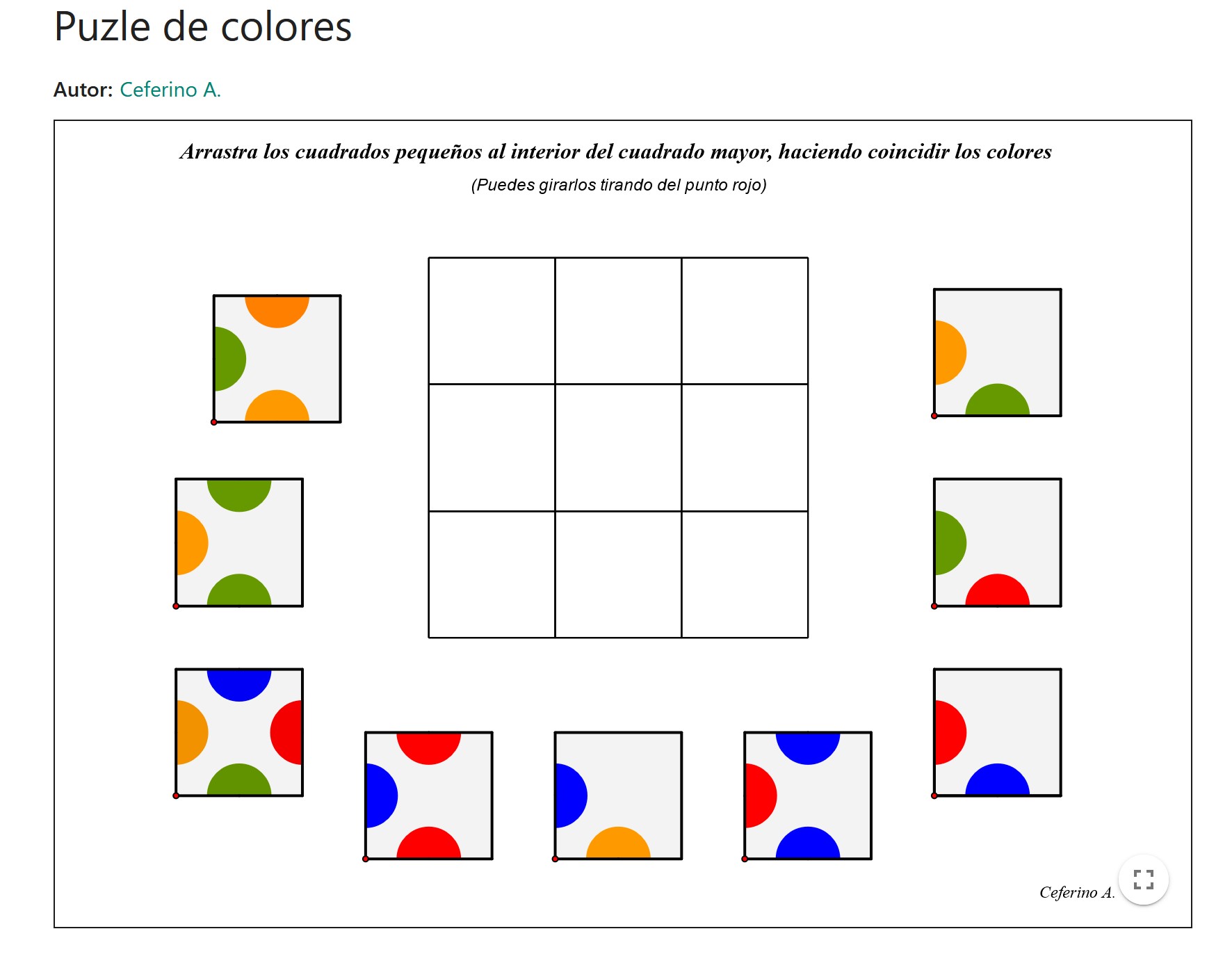
El applet presenta un puzle de nueve piezas que hay que colocar en una cuadrícula 3x3. Las piezas tienen partes de círculos de colores y hay que ubicar las piezas de tal manera que se encajen círculos del mismo color en todos los casos.
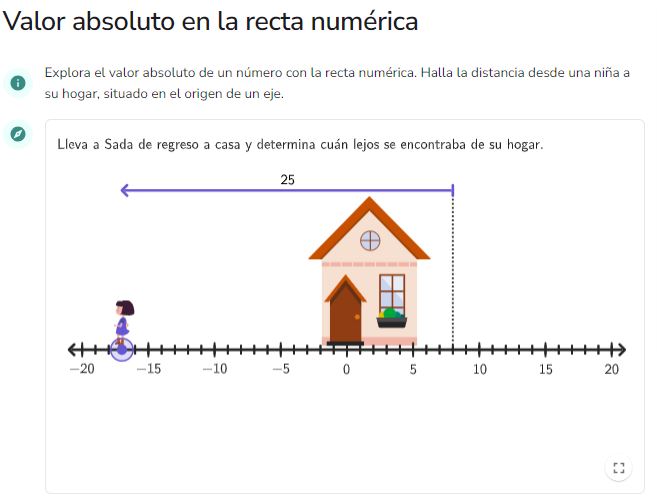
Valor absoluto en la recta numérica
El applet presenta la recta real sobre la que se sitúa en el origen una casa y una niña en cualquier otro lugar de la recta y se calcula la distancia a la que está de casa arrastrando la niña a su hogar. Es un recurso para iniciarse en el concepto de valor absoluto de un número a partir del cálculo de distancias en la recta real.
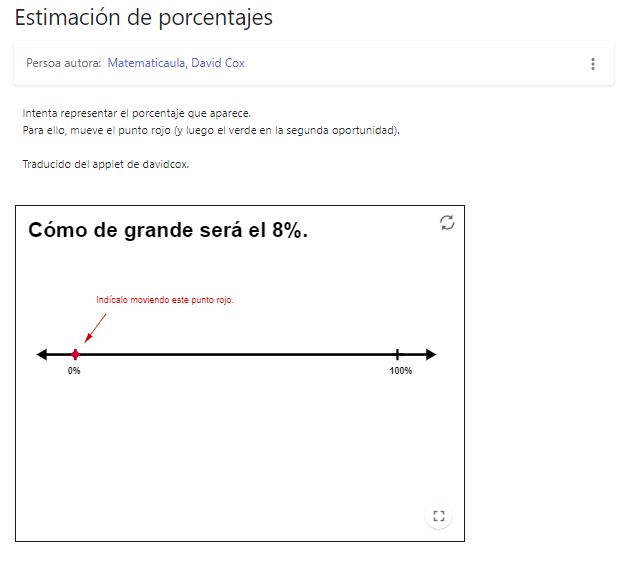
Estimación de porcentajes
El applet presenta un porcentaje y hay que situarlo de forma aproximada en la recta real, teniendo una segunda oportunidad de volver a ubicarlo en la recta. Así se muestra una vez situado el porcentaje el error de aproximación tanto de la primera opción como de la segunda.
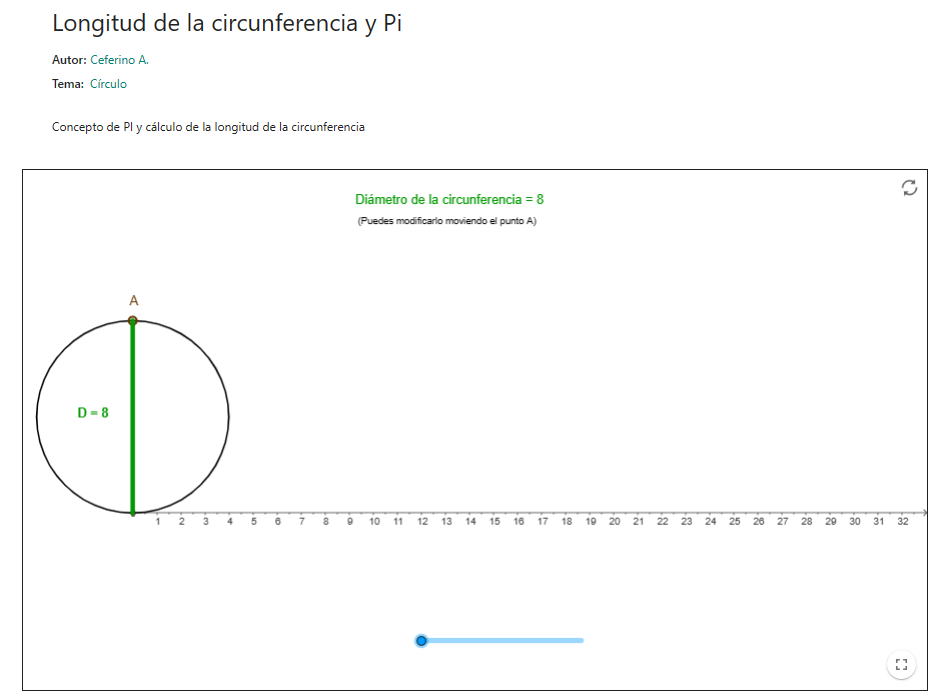
Longitud de la circunferencia y Pi
El applet presenta una circunferencia con el diámetro marcado y un deslizador que cuando se mueve la circunferencia se desliza dejando la huella de la longitud que recorre para favorecer la visualización de la relación que presenta la longitud de la circunferencia con el diámetro y el número Pi. Así se demuestra que la longitud de la circunferencia es Pi por el diámetro.