Buscador global
Mostrando del 781 al 790 de 2368 resultados para: Classroom: gestor de nuestras actividades de aula filtrando por: eXeLearning

De la dictadura a la democracia
La dictadura franquista se prolongó durante cerca de cuarenta años. En ellos se pueden apreciar diferentes periodos producidos por la evolución del régimen y por los cambios políticos, económicos y sociales que encontramos a nivel internacional. De esta manera hablaremos de un periodo de posguerra, de otro de consolidación del franquismo y de un último periodo de crisis antes del final de la dictadura. Encontrarás esta evolución en los tres primeros recursos del itinerario. En los otros tres recursos trabajaremos el periodo democrático posterior a la dictadura hasta nuestros días, empezando por la Transición a la democracia de los primeros años, continuando por el periodo de consolidación que supuso la alternancia de partidos en el poder y terminando con nuestra historia más reciente en este siglo XXI.
Parada 3: En caso de accidente
En este REA se profundiza en la prevención de riesgos laborales, así como el conocimiento del riesgo de incendio y riesgo eléctrico, así como en las medidas de emergencia y primeros auxilios.. Por otra parte, la finalidad de este recurso es contextualizar en cada ciclo formativo el análisis de los diferentes tipos de riesgos y la forma de protegerse contra los mismos.
- RA2. Alcanza las competencias necesarias para la obtención del título de Técnico Básico en Prevención de Riesgos Laborales.

Múltiplos en una cuadrícula de 100
El applet presenta los 100 primeros números naturales en una cuadrícula de 10x10, y donde a través de un deslizador (que puede tomar valores entre 1 y 20), se puede seleccionar un número dado y a partir de ahí, se van marcando los múltiplos de dicho número en la cuadrícula. De esta forma se pueden estudiar regularidades y patrones de dichos múltiplos.
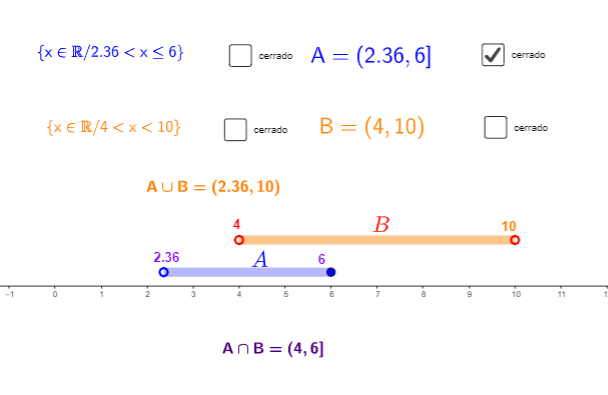
Intervalos. Operaciones de Unión e Intersección
Applet de GeoGebra que presenta el cálculo de la unión e intersección de distintos intervalos (abierto y cerrado) y su representación en la recta real.
14. Un panal de rica miel
Vamos a descubrir el gran mundo de las abejas (en castellano y en inglés) como un ejemplo de sociedad : sus tipos, su organización y la importancia de la polinización. Además buscaremos generar la sensibilización de niños y niñas sobre la importancia que tienen las abejas y otros polinizadores en la seguridad alimentaria y en la biodiversidad, tanto es así que el 20 de mayo de 2018, se celebró el primer Día Mundial de las Abejas como recordatorio. Observando la forma de los panales de las abejas nos adentramos en las matemáticas trabajando las principales formas geométricas : cuadrado, triángulo, rectángulo, pentágono y hexágono como polígonos regulares. Por último entraremos en una colmena para saber los secretos de cómo llega la miel al mercado.
Parada 17. Proyecto de innovación aplicada
Este REA tiene como principal objetivo alcanzar estos resultados del aprendizaje propios del módulo de IPE II:
- RA4. Identifica, define y valida ideas de emprendimiento generadoras de nuevas oportunidades a partir de estrategias de análisis del entorno socio productivo utilizando metodologías ágiles para el
emprendimiento. - RA5. Desarrolla un proyecto emprendedor de innovación social y/o tecnológica aplicada en colaboración con el entorno.
- RA4. Identifica, define y valida ideas de emprendimiento generadoras de nuevas oportunidades a partir de estrategias de análisis del entorno socio productivo utilizando metodologías ágiles para el

Números naturales de 6 cifras ( descomposición )
Applet que muestra la descomposición sumativa y multiplicativa de un número natural de 6 cifras.
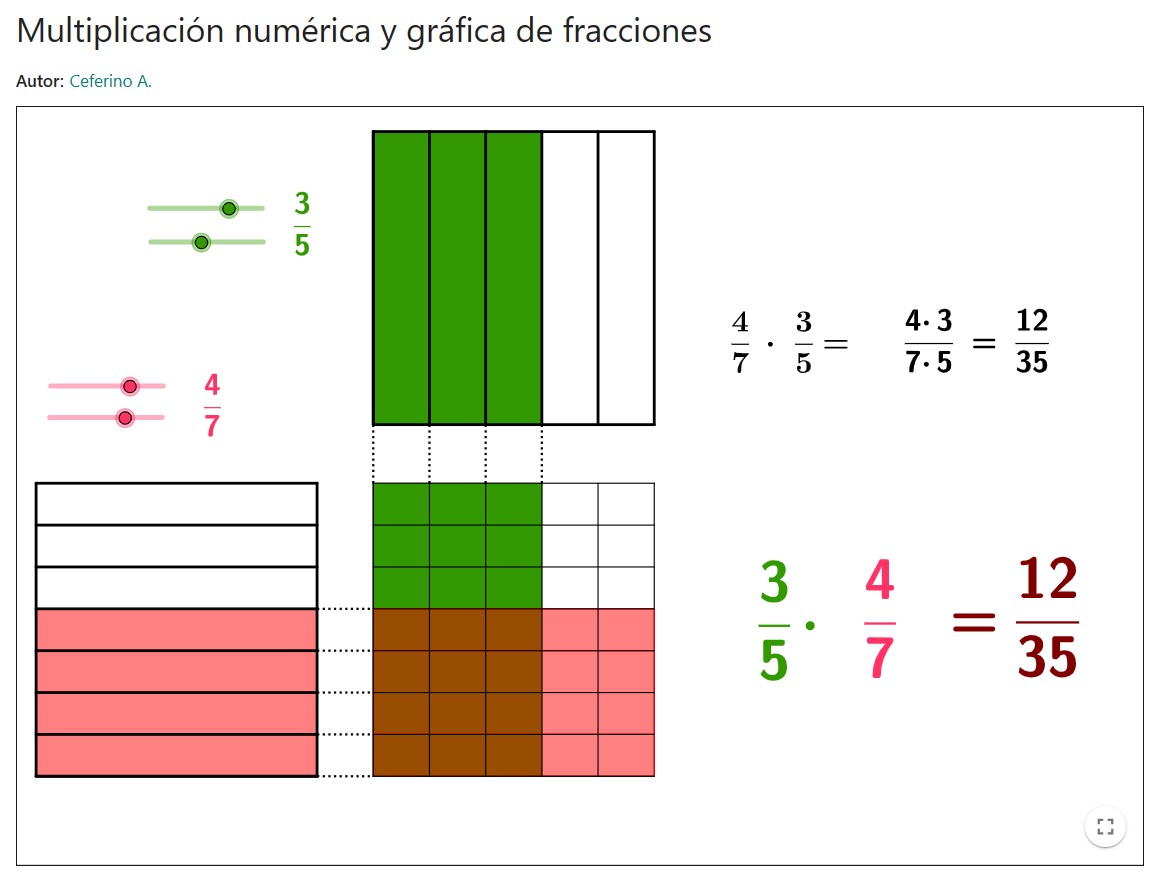
Multiplicación numérica y gráfica de fracciones
En este applet se representa gráficamente con el modelo de área la multiplicación de fracciones.

Ecuaciones de grado tres con denominadores
Applet con ejercicios autoevaluables para practicar la resolución de ecuaciones de tercer grado con denominadores.

Valor numérico de una expresión algebraica
Se proponen una serie de ejemplos en los que se explica qué es el valor numérico de una expresión algebraica. Se propone después que se calculen valores numéricos de expresiones algebraicas dadas. La puntuación se va acumulando dependiendo de los aciertos y errores.