Buscador global
Mostrando del 1 al 10 de 25 resultados para: Classroom: gestor de nuestras actividades de aula filtrando por: ESOTriángulos
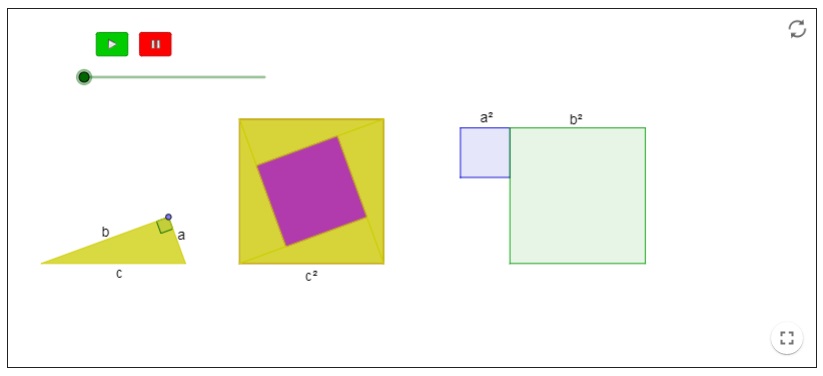
Teorema de Pitágoras. Demostración de Bhaskara
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. La superficie que abarca el cuadrado sobre la hipotenusa se desplaza hasta rellenar la suma de las superficies de los cuadrados sobre los catetos.
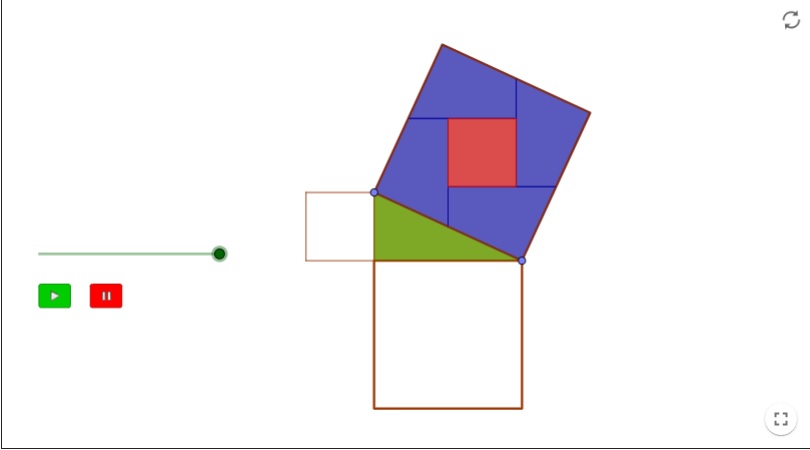
Teorema de Pitágoras. Demostración de Perigal
El recurso hace una demostración visual del Teorema de Pitágoras. El cuadrado sobre el cateto mayor se descompone en 4 cuadriláteros que se desplazan hasta el cuadrado sobre la hipotenusa. La superficie restante es la del cuadrado sobre el cateto pequeño.
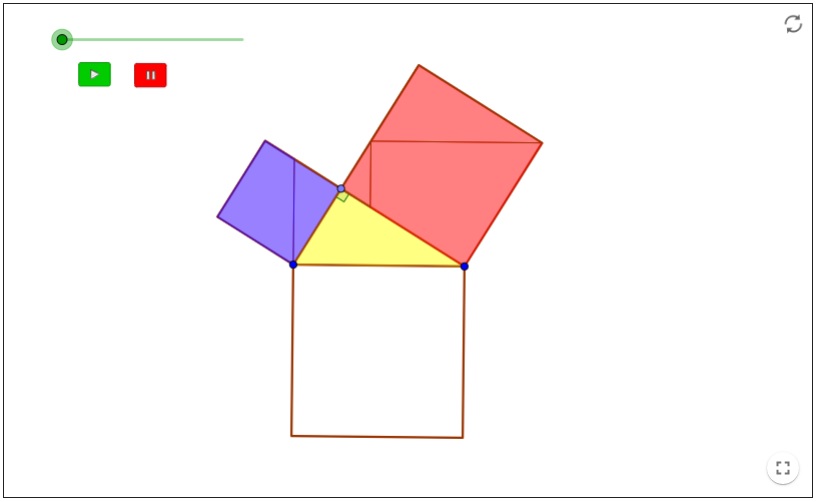
Teorema de Pitágoras. Demostración de Anaricio-Göpel
El recurso hace una demostración visual del Teorema de Pitágoras. El triángulo es variable dependiendo del vértice sobre el que se sitúa el ángulo recto. Las superficies que abarcan los cuadrados sobre los catetos se desplazan hasta completar la superficie del cuadrado sobre la hipotenusa, para lo que se descomponen en triángulos y cuadriláteros.
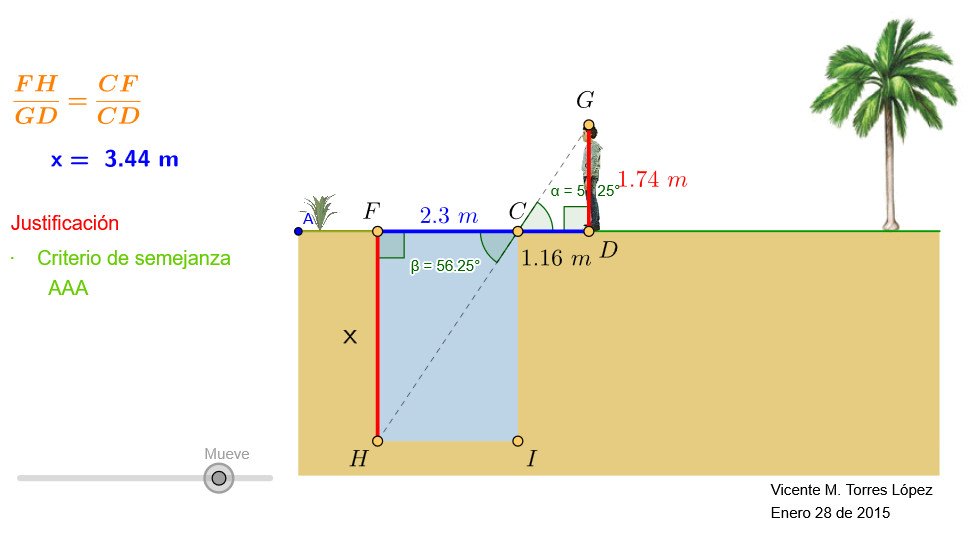
Cálculo de la profundidad de una piscina
En este applet se recrea una aplicación de la semejanza de triángulos, empleando herramientas que permiten calcular las profundidad de una piscina paso a paso, únicamente con la observación y medición de las distancias accesibles.

Teorema de Tales
Utiliza una situación práctica extrae los elementos para desarrollar una secuencia en varios pasos que explica el teorema de Thales.
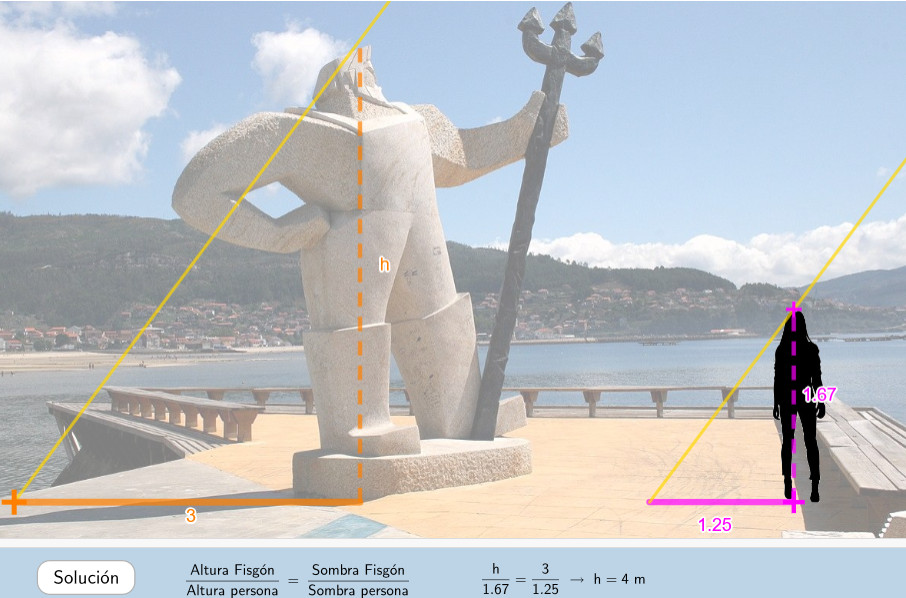
Cálculo de alturas por el método de Thales
Se trata de una aplicación de la semejanza que permite calcular la altura de una escultura utilizando el método de Thales.
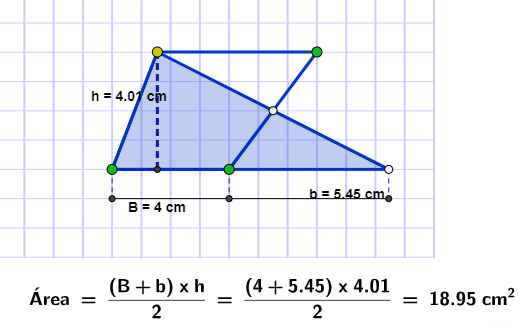
Áreas de polígonos (2º ESO)
Ejercicios para practicar áreas descomponiendo figuras para convertirlas en triángulos o rectángulos.

Teorema de Pitágoras
Applet de GeoGebra que realiza dos tipos de ejercicios. El cálculo del lado desconocido de un triángulo rectángulo. Y la determinación del tipo de triángulo según la longitud de los tres lados.
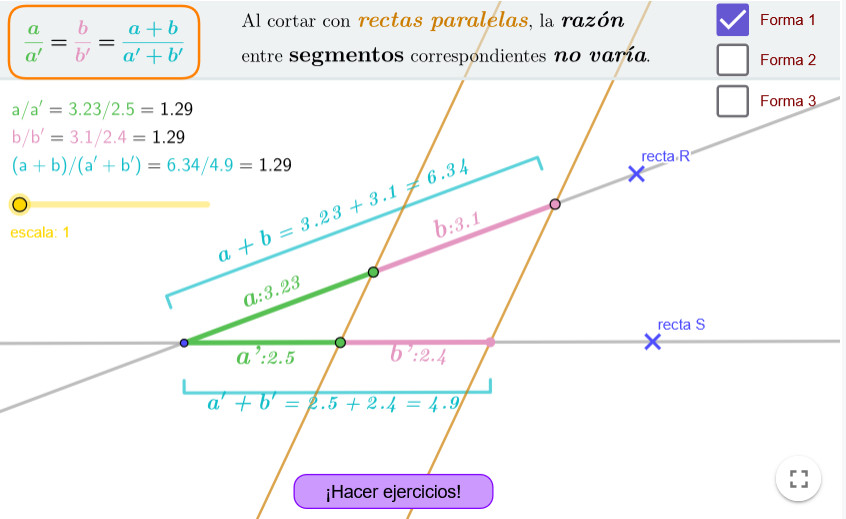
Teorema de Tales
Applet que presenta el Teorema de Tales exponiendo las distintas proporciones entre segmentos que pueden darse. A su vez, posibilita la práctica de la teoría con ejercicios autoevaluables.
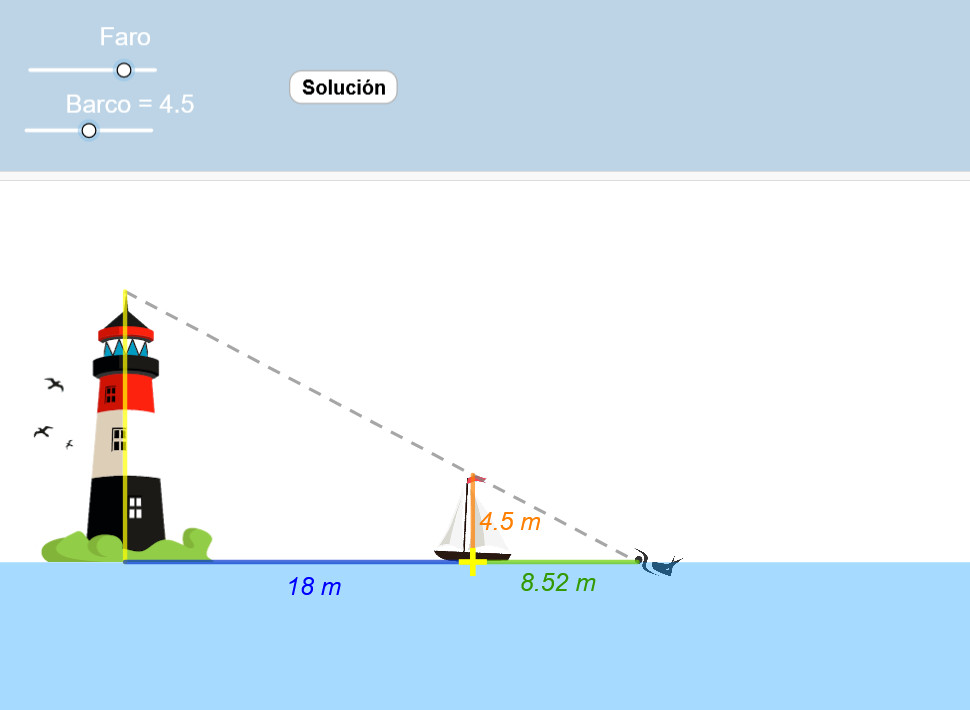
Cálculo de alturas (Triángulos en posición de Thales)
Se trata de una aplicación de la semejanza que permite calcular la altura de un faro mediante medidas indirectas y el uso del teorema de Tales.