Buscador global
Mostrando 9 de 9 resultados para: Classroom: gestor de nuestras actividades de aula filtrando por: Esfera
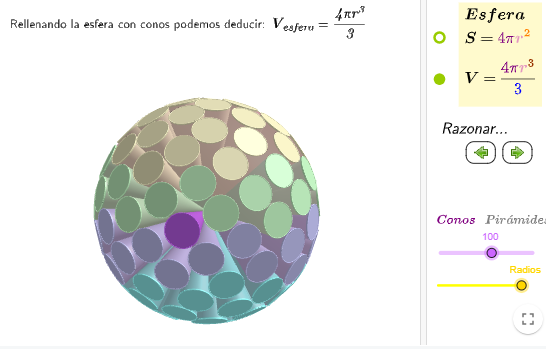
Volumen y superficie de la esfera
Applet de GeoGebra que permite deducir las fórmulas del volumen y de la superficie de la esfera a partir de conos y pirámides.
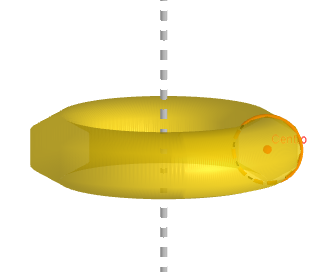
Superficies de Revolución
Permite generar cilindros, conos, esferas, troncos de conos, toros y otros cuerpos de revolución a partir de una línea poligonal cualquiera.
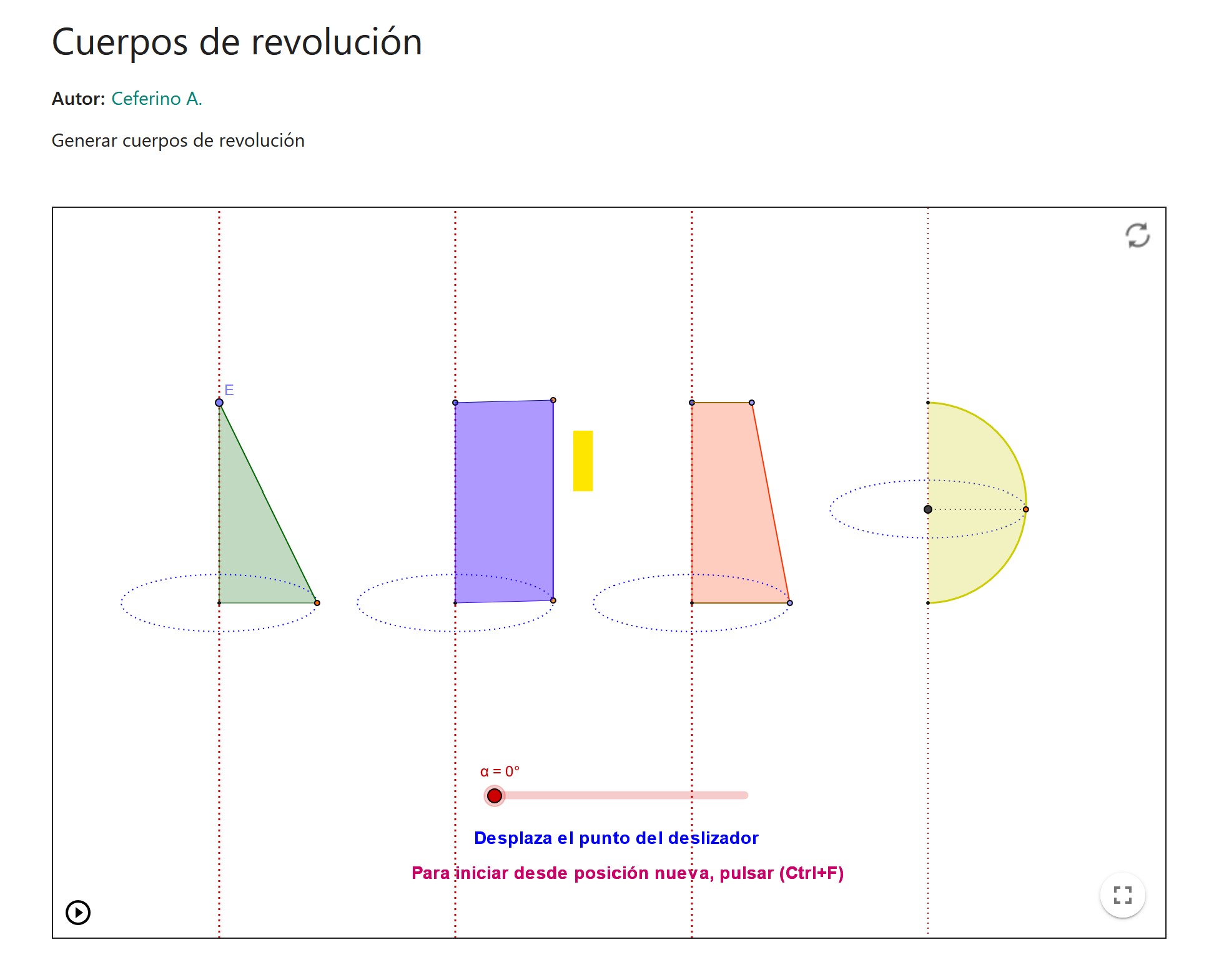
Cuerpos de revolución
El applet muestra las figuras planas a partir de las cuales, a través de la rotación en torno a una recta, se generan diferentes cuerpos de revolución (cono, cilindro, esfera, tronco de cono)
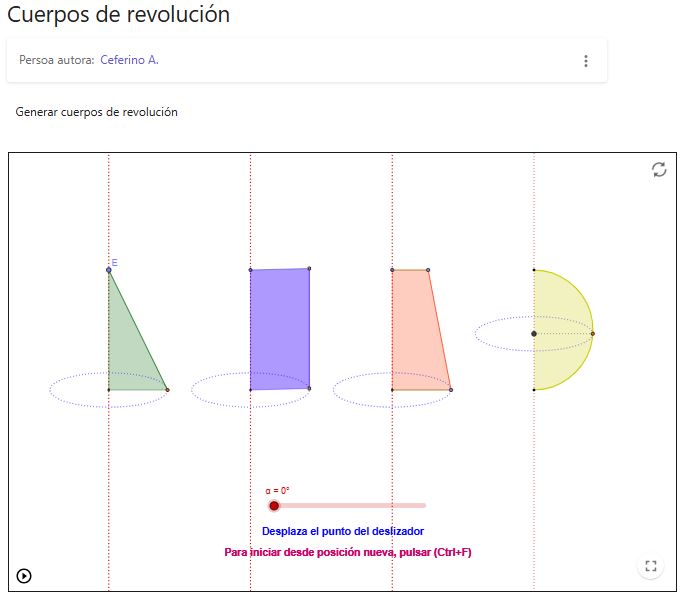
Cuerpos de revolución
Se representan diferentes figuras planas en una recta que al mover un deslizador generan diferentes figuras de revolución: cono, cilindro, tronco de cono y una esfera.
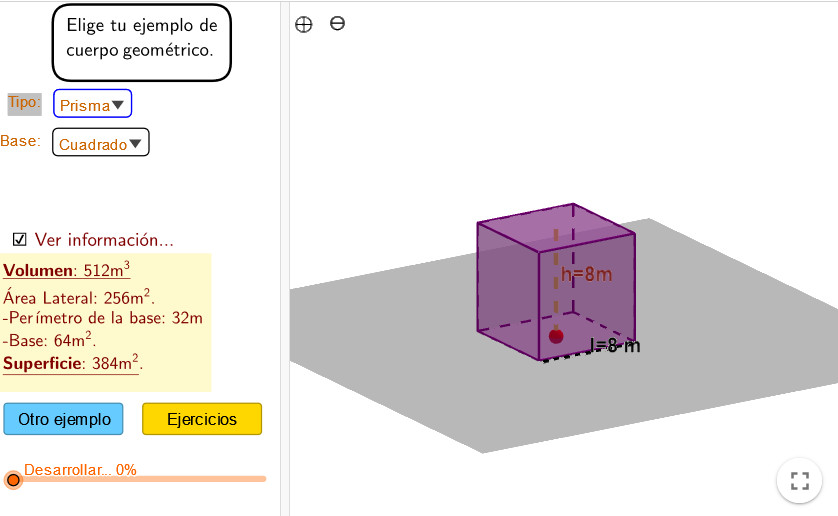
Volumen y superficie de cuerpos
Applet que muestra la forma de calcular la superficie y el volumen de prismas, pirámides y cuerpos de revolución y propone ejercicios autoevaluables al alumnado.
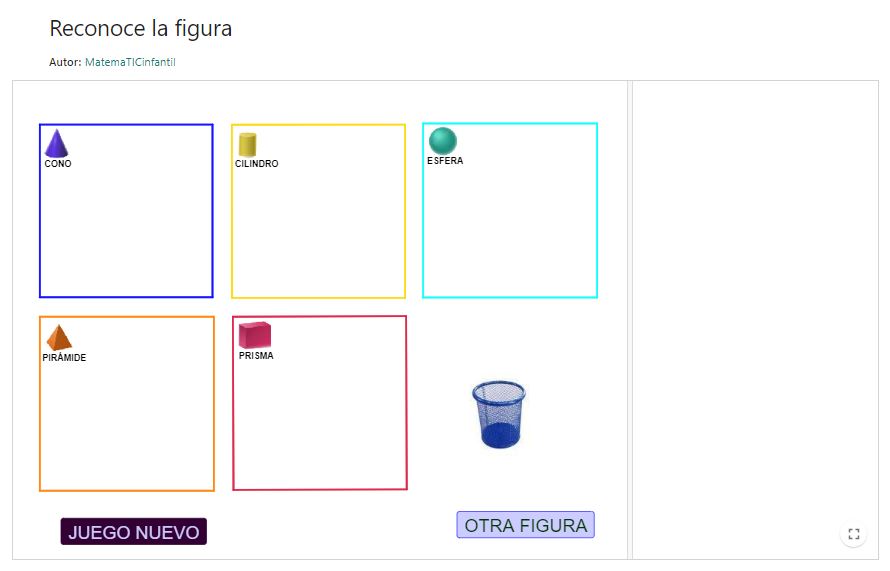
Reconoce la figura
Se presenta la imagen de una serie de objetos reales que evocan figuras tridimensionales que se tienen que identificar y agrupar según sea una esfera, un cono, un cilindro, una pirámide y un prisma. La imagen del objeto se tiene que arrastrar hacia el recuadro de la forma tridimensional que se identifica. Además si se hace clic sobre una de las figuras de los recuadros que se presentan, esta figura tridimensional aparece a la derecha de la escena ampliada en 3D. Cada vez que se da en el botón OTRA FIGURA aparece la imagen de otro objeto real, y cuando se agotan en el botón JUEGO NUEVO se reinicia y comienzan a salir de nuevo.

Intersección esfera-plano
Applet de Geogebra que presenta distintas formas de cortar una esfera, un cilindro y un cono con un plano que podemos colocar en distintas posiciones y orientaciones.

Visualización espacial
Applet de Geogebra que presenta distintas formas de cortar una esfera, un cilindro y un cono con un plano que podemos colocar en distintas posiciones y orientaciones.
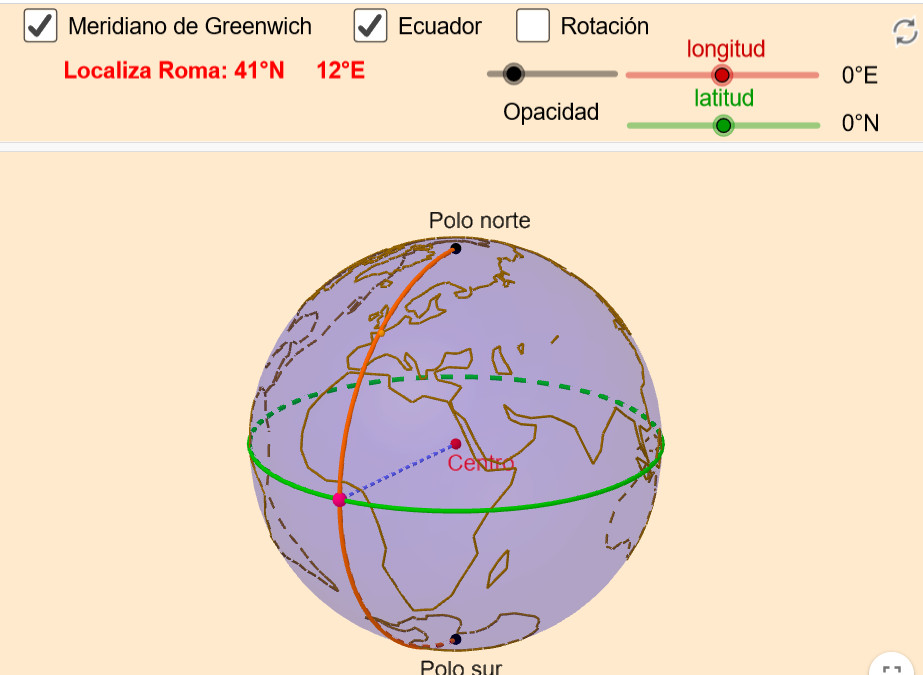
Coordenadas geográficas: localizando ciudades
Applet de GeoGebra que presenta una esfera sobre la que se han dibujado los continentes podemos desplazar un punto mediante dos deslizadores que controlan la longitud y la latitud.
- 1