Vídeo explicativo
Video descriptivo
Introducción Descarga artículo en PDF

- Responsable
- Isabel García Esteban
- Centro escolar
- Colegio San Vicente de Paul
- Dirección
- Plaza Virgen de la Vega 8
- Localidad y provincia
- Benavente. Zamora
- Web del centro
- Colegio San Vicente de Paul
- Contacto
- mariaisabel.garcia@sanvicentebenavente.es
- Etiquetas
- E.S.O.
- Matemáticas
- Flipped Classroom / Aula invertida
Utilizando los conceptos de Geometría Analítica en Matemáticas de 3º de ESO, los alumnos realizaron:
- Teselaciones en el plano, recreando los mosaicos de la Alhambra de Granada
- Spinners en movimiento, calculando áreas, perímetros, semejanza, simetrías y giros
- Movimientos en el plano, utilizando vectores y traslaciones
- Demostración geométrica del Teorema de Pitágoras
Los objetivos que me marqué a la hora de desarrollar este proyecto fueron:
- Integrar las herramientas TIC en el proceso de aprendizaje, no sólo en la búsqueda y análisis de la información, sino en la creación, interacción y dinaminación de conceptos a través del programa matemático GEOGEBRA, creando productos finales digitales
- Conectar las matemáticas con el entorno, hacer las matemáticas visibles. El alumno debe visualizar conceptos matemáticos, interpretarlos y resolverlos
- Aprender geometría a través de la experiencia
- Superar bloqueos, dificultades o inseguridades a situaciones desconocidas, utilizando herramientas TIC, que siempre son motivadoras para el alumno
- Generar confianza en las propias capacidades para desarrollar actitudes adecuadas y afrontar las dificultades propias del trabajo científico
- Integrar distintas competencias, además de la competencia matemática, se trabaja la competencia inter e intrapersonal, digital y social y cívica

Punto de partida
La experiencia se llevó a cabo en la asignatura de Matemáticas Académicas de 3º de ESO, en el Colegio San Vicente de Paúl de Benavente (Zamora). Ha sido desarrollada en el aula ordinaria y en el aula de informática de secundaria. El origen de la experiencia la desencadenó la moda de los Spinners. Todos los alumnos tenían uno y jugaban de vez en cuando con ellos. Me pareció la excusa perfecta e hilo conductor para trabajar la Geometría Analítica de 3º de ESO. Bajo el título “Retos Geométricos”, recopilamos los contenidos básicos de la geometría de las matemáticas de ese curso. Es básico que el alumno vea la utilidad y aplicación de las transformaciones geométricas en el entorno que le rodea, y en especial, en el arte.
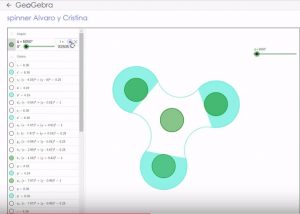
Los alumnos deben identificar las transformaciones en el plano, y la mejor forma de hacerlo, es a través de la manipulación y el descubrimiento. Para ello, el programa GeoGebra es la mejor opción, no sólo porque permite realizar dichos dibujos y transformaciones, sino, porque también permite movilidad en los procesos e interaccionar con ellos, a través de deslizadores y comandos especiales. Esta característica del programa es su punto fuerte, que el alumno sea capaz de construir geometría y “dar vida”a sus construcciones, facilita la comprensión de procesos y conceptos, fomenta la autonomía y favorece la capacidad de superación personal. Además, permite actividades multinivel, es decir, se adapta a las capacidades del alumno, ya que las construcciones pueden ser más o menos complejas, marcando unos mínimos en cada una de ellas, el alumno es libre de investigar y avanzar si puede. Se define el aprender haciendo; el alumno planifica y construye el aprendizaje. Los materiales y recursos utilizados fueron: el libro de texto, GeoGebra, vídeos flipped, fotografías, spinners, información en red.
Paso a Paso
El proyecto “Retos Geométricos” ha sido desarrollado a través de la metodología Flipped Learning, además ha estado el presente el trabajo cooperativo, individual y por parejas. Este proyecto está programado para llevarse a cabo en 12 sesiones de trabajo y los materiales que se han utilizado en el proceso son:
- Libro de texto
- Fotografías y documentación sobre los mosaicos de la Alhambra de Granada
- Vídeos flipped sobre conceptos teóricos
- Videotutoriales sobre construcción de elementos geométricos con GeoGebra
- Programa informático GeoGebra
Paso 1
Trabajamos las traslaciones, giros y simetrías

Flipped y sesiones activas. El proyecto se ayudó de la metodología Flipped, que nos sirvió para liberar tiempo de clase dedicado a la teoría, y volcarnos en el aprendizaje activo. Los alumnos trabajaban vídeos en casa, para después realizar ejercicios en clase, de forma cooperativa mediante técnicas específicas (lápices al centro, 1-2-4, folio giratorio, cabezas pensantes, etc) o de forma individual. Duración: 5 sesiones.
Paso 2
Conectando con el entorno

Después de trabajar en el aula ordinaria los contenidos del currículo y realizar ejercicios prácticos básicos, se realizó la primera sesión en el aula de Informática. A partir de ese momento, invité a los alumnos a realizar un proyecto por parejas (los compañeros de hombro de los grupos cooperativos). Indicando qué ibamos a trabajar, cuál sería el producto final y cómo lo iba a evaluar. En este paso 2, los alumnos debían planificar su trabajo. Buscar información sobre los mosaicos de la Alhambra de Granada, buscar geometría y movimientos en el arte, etc. La duración de este proceso fue de 1 sesión.
Paso 3
Creamos el producto final
En el aula de Informática, los alumnos por parejas crean sus construcciones en GeoGebra. Los retos fueron los siguientes:
- Reto 1: Diseñamos un Spinner. Aplicamos simetría central, giros, deslizadores.
- Reto 2: Movimientos en el plano. Aplicamos vectores, traslación, giros, etc.
- Reto 3: Teselas de la Alhambra de Granada. Reproducimos teselas de la Alhambra, aplicamos simetría central, simetría axial, traslaciones y giros sucesivos.
- Reto 4: Teorema de Pitágoras. Realizamos una construcción dinámica para demostrar de forma geométrica el Teorema de Pitágoras.

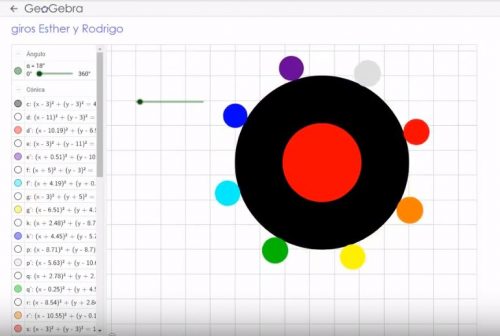
En estos 4 retos, se resume todo lo que hemos visto de Geometría del Plano y Geometría Analítica. El alumno debe poner en práctica lo aprendido. Además de conocimientos matemáticos, es una actividad competencial. Trabajamos la competencia de aprender a aprender, la competencia social y cívica, la intrapersonal e interpersonal y la lingüística.
Los alumnos trabajaban de forma autónoma, ayudándose del profesor, que tiene el rol de guía y supervisión del trabajo. Además de lo aprendido en las sesiones anteriores, se ayudaron de dos tutoriales que creé para el proyecto:
- Construcción de un mosaico Hueso Nazarí con Geogebra
- Teselando el plano, con la pajarita Nazarí con Geogebra

Paso 4
Los alumnos expusieron sus productos finales al grupo- clase. Los trabajos se enlazaron en un Padlet y se creó un vídeo recopilatorio de los mejores retos.
El trabajo se incluyó en la programación didáctica como proyecto de final de evaluación durante el tercer trimestre.
Evaluamos
La evaluación se realizó a lo largo de todo el proceso. Este proceso tuvo en cuenta los tres espacios que se generaron:
- En el espacio individual, se realizó una evaluación basándonos en los cuestionarios, Edpuzzle, y la observación directa en el aula.
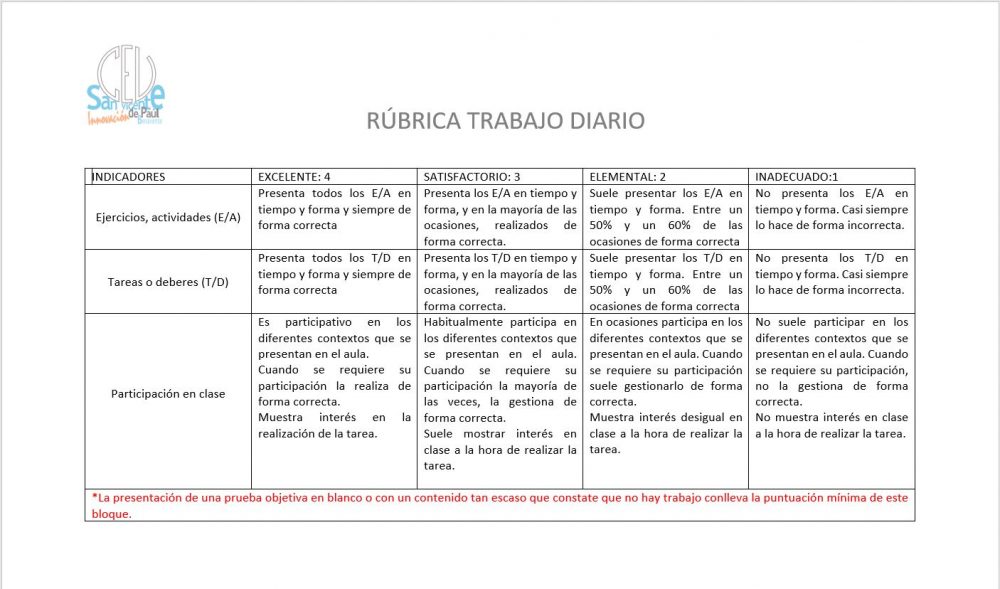
- En el espacio cooperativo, se tuvo en cuenta las actividades en el aula que apoyaron al proyecto, utilizando la rúbrica que tenemos de trabajo en clase.
- El trabajo por parejas que se realizó para el producto final, se realizó a través de las rúbricas de trabajo digital y la rúbrica de expresión oral (presentación en grupo clase).
El éxito de la experiencia radica en el peso del trabajo final en la evaluación. El alumno debe saber su valor y su peso en la nota final de evaluación. No podemos pretender que los alumnos realicen trabajos excepcionales, si después no valoramos lo suficiente el esfuerzo y tiempo empleado por el alumno.
Conclusiones
El poryecto se adapta al almuno, no el alumno al proyecto
- Los alumnos trabajan a su propio ritmo.
- El grado de complejidad de las construcciones puede ser muy diferente. Aunque se marcaron unos mínimos, los propios alumnos buscaban maneras de realizarlos. Probaban, se retaban, intentaban superarse…
- El proyecto permite adaptarse a las capacidades de los alumnos. Por ejemplo, no todos los mosaicos de la Alhambra son igual de complejos, los alumnos eran libres de elegir su mosaico para recrearlo.
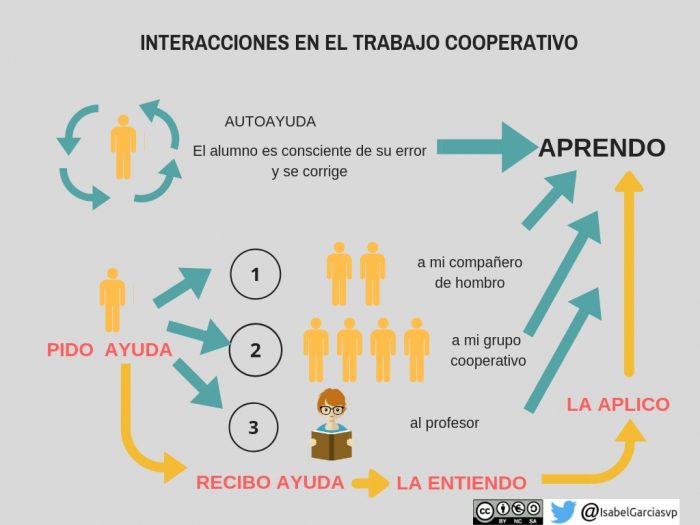
El alumno mejora su aprendizaje porque:
- Se combina trabajo individual, trabajo cooperativo y trabajo por parejas. Las distintas formas de agrupar y secuenciar trabajos aumentan el grado de interacción y favorecen el aprendizaje.
- El trabajo digital siempre motiva al alumno. Si el alumno está motivado, está predispuesto a aprender.
- El alumno debe adquirir la competencia digital, integrándola con los elementos del currículo.
¿Te animas?
¿Cómo puedo empezar?
Utilizar GeoGebra para realizar proyectos matemáticos es altamente recomendable. Podemos acceder a múltiples proyectos compartidos en la red utilizando esta herramienta. Existen muchos tutoriales sobre la herramienta, en Youtube. También podemos acceder a recursos y libros de GeoGebra si nos registramos en su web oficial.
Existen numerosos profesores que lo utilizan y tienen muchos recursos creados. Entre los más relevantes destaco:
- Juan Franciso Hernández @juanfisicahr en Twitter y su blog «Esto no entra en el examen».
- Alejandro Gallardo @alegallardo28 con numerosas construcciones desde la web GeoGebra.
- Antonio Aomatos @aomatos en Twitter.
¿Qué dificultades pueden surgir o han surgido?
Los alumnos tienen distintos niveles de conocimiento de la herramienta GeoGebra. Pueden surgir dificultades, pero se resuelven fácilmente por el profesor, y mejor entre compañeros.
¿Por qué recomendarías a otros profesores llevar a cabo experiencias similares?
Porque la motivación del alumnado aumenta. Los alumnos agradecen ese cambio en la manera de aprender, y están expectantes y predispuestos a aprender. Los alumnos, en condiciones favorables, SIEMPRE nos sorprenden. Si nosotros damos lo mejor de nosotros y ellos así lo perciben, ellos también nos responden de la misma manera.

Materiales complementarios
Información Copyright
“Retos Geométricos” por Isabel García Esteban para INTEF
Obra publicada con Licencia Creative Commons Reconocimiento-Compartir Igual 4.0
NIPO (web) 847-19-120-X
ISSN (web) 2695-4184
DOI (web) 10.4438/2695-4184_EEI_2019_847-19-120-X
NIPO (formato html) 847-19-132-2
NIPO (formato pdf) 847-19-133-8
DOI (formato pdf) 10.4438/2695-4184_EEIpdf6_2019_847-19-133-8
———————————
Para cualquier asunto relacionado con esta publicación contactar con:
Instituto Nacional de Tecnologías Educativas y de Formación del Profesorado
C/Torrelaguna, 58. 28027 Madrid.
Tfno.: 91-377 83 00. Fax: 91-368 07 09
Correo electrónico: cau.recursos.intef@educacion.gob.es